【题目】如果定义在(﹣∞,0)∪(0,+∞)上的奇函数f(x),在(0,+∞)内是减函数,又有f(3)=0,则xf(x)<0的解集为( )
A.{x|﹣3<x<0或x>3}
B.{x|x<﹣3或0<x<3}
C.{x|﹣3<x<0或0<x<3}
D.{x|x<﹣3或x>3}
参考答案:
【答案】D
【解析】解:不等式xf(x)<0等价为 ![]() .
.
因为函数y=f(x)为奇函数,且在(0,+∞)上是减函数,又f(3)=0,
所以解得x>3或x<﹣3,
即不等式的解集为{x|x<﹣3或x>3}.
故选:D.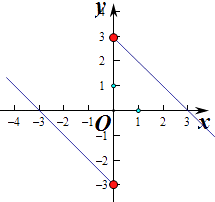
【考点精析】通过灵活运用奇偶性与单调性的综合,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,既是偶函数,又在(0,+∞)单调递增的函数是( )
A.y=﹣x2
B.y=2﹣|x|
C.y=| |
|
D.y=lg|x| -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩(环)如下:

(1)用茎叶图表示甲、乙两个人的成绩;
(2)根据茎叶图分析甲、乙两人的成绩;
(3)计算两个样本的平均数
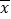 和标准差
和标准差 ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程 .
.(1)若
 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数,  是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
 时从区间
时从区间 上任取的一个数,
上任取的一个数,  是从区间
是从区间 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
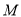 :
: 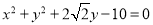 和点
和点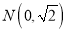 ,动圆
,动圆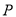 经过点
经过点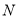 且与圆
且与圆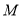 相切,圆心
相切,圆心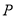 的轨迹为曲线
的轨迹为曲线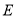 .
.(1)求曲线
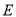 的方程;
的方程;(2)点
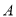 是曲线
是曲线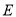 与
与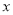 轴正半轴的交点,点
轴正半轴的交点,点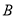 ,
, 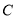 在曲线
在曲线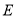 上,若直线
上,若直线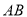 ,
, 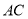 的斜率分别是
的斜率分别是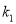 ,
, 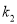 ,满足
,满足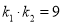 ,求
,求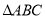 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x , x∈(0,2)的值域为A,函数g(x)=log2(x﹣2a)+
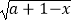 (a<1)的定义域为B.
(a<1)的定义域为B.
(1)求集合A,B;
(2)若BA,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区拟建立一个艺术博物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从
 个招标问题中随机抽取
个招标问题中随机抽取 个问题,已知这
个问题,已知这 个招标问题中,甲公司可正确回答其中的
个招标问题中,甲公司可正确回答其中的 道題目,而乙公司能正确回答毎道题目的概率均为
道題目,而乙公司能正确回答毎道题目的概率均为 ,甲、乙两家公司对每题的回答都是相互独立,互不影响的.
,甲、乙两家公司对每题的回答都是相互独立,互不影响的.(1)求甲、乙两家公司共答对
 道题目的概率;
道题目的概率;(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
相关试题

