【题目】在直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的焦点为
的焦点为![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(Ⅰ)求椭圆![]() 的离心率;
的离心率;
(Ⅱ)设![]() 的斜率为
的斜率为![]() ,在椭圆
,在椭圆![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() (2)不存在点
(2)不存在点![]() ,使
,使![]() 成立.
成立.
【解析】试题分析:(1)根据椭圆定义得![]() 的周长为
的周长为![]() ,即
,即![]() ,解得椭圆
,解得椭圆![]() 的离心率;(2)设
的离心率;(2)设![]() ,
, ![]() ,
, ![]() ,则由
,则由![]() 得
得![]() 代入等式
代入等式![]() ,并化简得
,并化简得![]() .利用直线方程
.利用直线方程![]() 与椭圆方程联立方程组,结合韦达定理得
与椭圆方程联立方程组,结合韦达定理得![]() ,
, ![]() .代入解得矛盾,故不存在.
.代入解得矛盾,故不存在.
试题解析:解:(Ⅰ)∵椭圆![]() :
: ![]() 的焦点为
的焦点为![]() ,
, ![]() ,
,
过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,
两点,
![]() 的周长为短轴长的
的周长为短轴长的![]() 倍,
倍, ![]() 的周长为
的周长为![]() .
.
∴依题意知![]() ,即
,即![]() .
.
∴椭圆![]() 的离心率
的离心率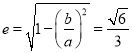 .
.
(Ⅱ)设椭圆方程为![]() ,
,
直线的方程为![]() ,
,
代入椭圆方程得![]() .
.
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
设![]() ,则
,则![]() .①
.①
由![]() 得
得![]()
代入①得![]() .
.
因为![]() ,
, ![]() ,
,
所以![]() .②
.②
而![]()
![]() .
.
从而②式不成立.
故不存在点![]() ,使
,使![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次数学考试试题中共有
 道选择题,每道选择题都有
道选择题,每道选择题都有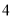 个选项,其中仅有一个是正确的.评分标准规定:“每题只选
个选项,其中仅有一个是正确的.评分标准规定:“每题只选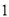 项,答对得
项,答对得 分,不答或答错得
分,不答或答错得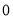 分.”某考生每道题都给了一个答案,已确定有
分.”某考生每道题都给了一个答案,已确定有 道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:
道题的答案是正确的,而其余题中,有两道题都可判断出两个选项是错误的有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜,试求出该考生:(Ⅰ)得
 分的概率;
分的概率;(Ⅱ)所得分数
 的数学期望.
的数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lg(1+x)+lg(1﹣x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性;
(3)求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段
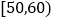 ,
,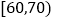 ,…,
,…,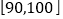 后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如图部分频率分布直方图.观察图形的信息,回答下列问题: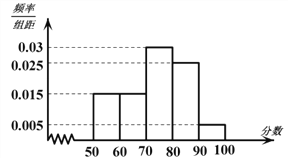
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
 +
+  的定义域为( )
的定义域为( )
A.[﹣2,0)∪(0,2]
B.(﹣1,0)∪(0,2]
C.[﹣2,2]
D.(﹣1,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,既是偶函数,又在(0,+∞)单调递增的函数是( )
A.y=﹣x2
B.y=2﹣|x|
C.y=| |
|
D.y=lg|x| -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次运动会中甲、乙两名射击运动员决赛中各射击十次的成绩(环)如下:

(1)用茎叶图表示甲、乙两个人的成绩;
(2)根据茎叶图分析甲、乙两人的成绩;
(3)计算两个样本的平均数
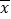 和标准差
和标准差 ,并根据计算结果估计哪位运动员的成绩比较稳定.
,并根据计算结果估计哪位运动员的成绩比较稳定.
相关试题

