【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.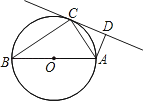
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
参考答案:
【答案】
(1)
证明:连接OC,如图所示:

∵AB是⊙O直径,
∴∠ACB=90°,
∵OB=OC,
∴∠B=∠BCO,
又∵∠ACD=∠B,
∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,
即OC⊥CD,
∴CD是⊙O的切线;
(2)
解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,
又∵∠ACD=∠B,
∴△ACB∽△ADC,
∴AC2=ADAB=1×4=4,
∴AC=2.
【解析】本题考查了切线的判定、等腰三角形的性质、相似三角形的判定与性质;熟练掌握切线的判定,证明三角形相似是解决问题(2)的关键.(1)连接OC,由圆周角定理得出∠ACB=90°,由等腰三角形的性质得出∠B=∠BCO,证出∠OCD=∠OCA+∠BCO=∠ACB=90°,即可得出结论;(2)证明△ACB∽△ADC,得出AC2=ADAB,即可得出结果.
【考点精析】掌握切线的判定定理是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,
 表示开业第
表示开业第 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
经过进一步的统计分析,发现
 与
与 具有线性相关关系.
具有线性相关关系.(1)根据上表给出的数据,用最小二乘法,求出
 与
与 的线性回归方程
的线性回归方程 ;
;(2)若该分店此次抽奖活动自开业始,持续10天,参加抽奖的每位顾客抽到一等奖(价值200元奖品)的概率为
 ,抽到二等奖(价值100元奖品)的概率为
,抽到二等奖(价值100元奖品)的概率为 ,抽到三等奖(价值10元奖品)的概率为
,抽到三等奖(价值10元奖品)的概率为 ,试估计该分店在此次抽奖活动结束时送出多少元奖品?
,试估计该分店在此次抽奖活动结束时送出多少元奖品?参考公式:
 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,侧面
中,侧面 底面
底面 ,
, ,
, ,且
,且 ,点
,点 ,
, ,
, 分别为
分别为 ,
, ,
, 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 .
.(Ⅱ)求证:
 平面
平面 .
.(Ⅲ)写出四棱锥
 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由) -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥S-ABCD中,底面ABCD为菱形,SD⊥平面ABCD,点E为SD的中点.
(1)求证:直线SB∥平面ACE
(2)求证:直线AC⊥平面SBD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, 为
为 的中点,
的中点,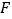 为线段
为线段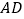 上的一点,且
上的一点,且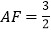 .现将四边形
.现将四边形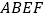 沿直线
沿直线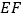 翻折,使翻折后的二面角
翻折,使翻折后的二面角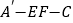 的余弦值为
的余弦值为 .
.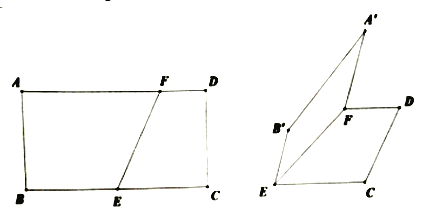
(1)求证:
 ;
;(2)求直线
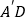 与平面
与平面 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的对称轴为坐标轴,离心率为
的对称轴为坐标轴,离心率为 ,且一个焦点坐标为
,且一个焦点坐标为 .
.
(1)求椭圆
 的方程;
的方程;(2)设直线
 与椭圆
与椭圆 相交于
相交于 两点,以线段
两点,以线段 为邻边作平行四边形
为邻边作平行四边形 ,其中点
,其中点 在椭圆
在椭圆 上,
上,  为坐标原点,求点
为坐标原点,求点 到直线
到直线 的距离的最小值.
的距离的最小值.
相关试题

