【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列和期望E(X).
参考答案:
【答案】(1)![]() ;(2)分布列见解析,期望为16.
;(2)分布列见解析,期望为16.
【解析】试题分析:
(1)利用对立事件公式可得该顾客中奖的概率为![]() ;
;
(2)由超几何分布求得分布列,然后求解数学期望可得期望值为16.
试题解析:
解法一:(1)P=I-![]() =1-
=1-![]() =
=![]() ,即该顾客中奖的概率为
,即该顾客中奖的概率为![]() .
.
(2)ξ的所有可能值为:0,10,20,50,60(元).P(ξ=0)=![]() =
=![]() ,P(ξ=10)=
,P(ξ=10)=![]() =
=![]() ,
,
P(ξ=20)=![]() =
=![]() ,P(ξ=50)=
,P(ξ=50)=![]() =
=![]() ,P(ξ=60)=
,P(ξ=60)=![]() =
=![]() .
.
ξ | 0 | 10 | 20 | 50 | 60 |
P |
|
|
|
| bn= 8an+1an-16an+1+2an+5=0, |
故ξ有分布列:
从而期望Eξ=0×![]() +10×
+10×![]() +20×
+20×![]() +50×
+50×![]() +60×
+60×![]() =16.
=16.
解法二:(1)P=![]() =
=![]() =
=![]() ,
,
(2)ξ的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值Eξ=2×8=16(元).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.

(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,曲线
 与x轴交于不同的两点A,B,曲线Γ与y轴交于点C.
与x轴交于不同的两点A,B,曲线Γ与y轴交于点C.(1)是否存在以AB为直径的圆过点C?若存在,求出该圆的方程;若不存在,请说明理由;
(2)求证:过A,B,C三点的圆过定点,并求出该定点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知变量
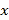 之间的线性回归方程为
之间的线性回归方程为 ,且变量
,且变量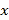 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )x
6
8
10
12
y
6
m
3
2
A. 变量
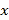 之间呈现负相关关系
之间呈现负相关关系B.
 的值等于5
的值等于5C. 变量
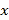 之间的相关系数
之间的相关系数
D. 由表格数据知,该回归直线必过点(9,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA=
 ,cosC=
,cosC= 

(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 是定义在
是定义在 上的可导函数,其导函数为
上的可导函数,其导函数为 ,且有
,且有 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为a,公差为d的等差数列(d≠0),Sn是其前n项和.记bn=
 ,n∈N* , 其中c为实数.
,n∈N* , 其中c为实数.
(1)若c=0,且b1 , b2 , b4成等比数列,证明:Snk=n2Sk(k,n∈N*);
(2)若{bn}是等差数列,证明:c=0.
相关试题

