【题目】在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sin θ,θ∈[0,2π).
(1)求曲线C的直角坐标方程;
(2)在曲线C上求一点D,使它到直线l:![]() 的距离最短,并求出点D的直角坐标.
的距离最短,并求出点D的直角坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用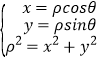 可把圆C的极坐标方程化为普通方程.
可把圆C的极坐标方程化为普通方程.
(2)利用圆的几何性质即可得到结果.
(1)由ρ=2sin θ,θ∈[0,2π),可得ρ2=2ρsin θ.
因为ρ2=x2+y2,ρsin θ=y,
所以曲线C的直角坐标方程为x2+(y-1)2=1.
(2)因为曲线C:x2+(y-1)2=1是以C(0,1)为圆心、1为半径的圆,易知曲线C与直线l相离.
设点D(x0,y0),且点D到直线l:y=-![]() x+5的距离最短,
x+5的距离最短,
所以曲线C在点D处的切线与直线l:y=-![]() x+5平行.
x+5平行.
即直线CD与l的斜率的乘积等于-1,
即![]() ×(-
×(-![]() )=-1,又x+(y0-1)2=1,
)=-1,又x+(y0-1)2=1,
可得x0=-![]() (舍去)或x0=
(舍去)或x0=![]() ,所以y0=
,所以y0=![]() ,
,
即点D的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设不等式|2x﹣1|<1的解集为M,a∈M,b∈M
(1)试比较ab+1与a+b的大小
(2)设max表示数集A的最大数,h=max{ ,
,  ,
,  },求证h≥2.
},求证h≥2. -
科目: 来源: 题型:
查看答案和解析>>【题目】极坐标系中椭圆C的方程为ρ2=
 ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)求该椭圆的直角标方程,若椭圆上任一点坐标为P(x,y),求x+ y的取值范围;
y的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率;
(2)两数中至少有一个奇数的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知PA与圆O相切于点A,经过点O的割线PBC交圆O于点B,C,∠APC的平分线分别交AB,AC于点D,E.
(Ⅰ)证明:∠ADE=∠AED;
(Ⅱ)若AC=AP,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将函数y=sin2x的图象先向左平移
 个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
个单位长度,然后将所有点的横坐标变为原来的2倍(纵坐标不变),则所得到的图象对应函数解析式为( )
A.
B.y=2cos2x
C.y=2sin2x
D.y=cosx -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:平均每天喝500ml以上为常喝,体重超过50kg为肥胖。
常喝
不常喝
合计
肥胖
6
2
8
不肥胖
4
18
22
合计
10
20
30
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为
 。
。(1)是否有
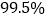 的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
的把握认为肥胖与常喝碳酸饮料有关?说明你的理由(2)现从常喝碳酸饮料且肥胖的学生中(2名女生),抽取2人参加电视节目,则正好抽到一男一女的概率是多少?
参考数据:

(参考公式:
 ,其中
,其中 )
)
相关试题

