【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
参考答案:
【答案】D
【解析】解:根据题意得,用分层抽样在各层中的抽样比为 ![]() =
= ![]() , 则在高一年级抽取的人数是900×
, 则在高一年级抽取的人数是900× ![]() =45人,高二年级抽取的人数是1200×
=45人,高二年级抽取的人数是1200× ![]() =60人,
=60人,
高三年级抽取的人数是600× ![]() =30人,
=30人,
那么高一、高二、高三各年级抽取的人数分别为45,60,30.
故选D.
根据分层抽样的定义求出在各层中的抽样比,即样本容量比上总体容量,按此比例求出在各年级中抽取的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,根据如图的框图所打印出数列的第四项是

-
科目: 来源: 题型:
查看答案和解析>>【题目】北京市的士收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里收2.6元,另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的流程图如图所示,则①处应填( )
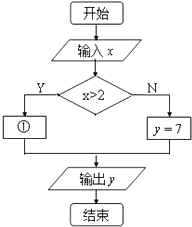
A.y=7+2.6x
B.y=8+2.6x
C.y=7+2.6(x﹣2)
D.y=8+2.6(x﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 且满足a1=
 ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)猜想Sn的表达式,并用数学归纳法证明;
(2)设bn= ,n∈N* , 求bn的最大值.
,n∈N* , 求bn的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l过点P(3,6)且与x,y轴的正半轴分别交于A、B两点,O是坐标原点,则当|OA|+|OB|取得最小值时的直线方程是(用一般式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知位置向量
 =(log2(m2+3m﹣8),log2(2m﹣2)),
=(log2(m2+3m﹣8),log2(2m﹣2)),  =(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y=
=(1,0),若以OA、OB为邻边的平行四边形OACB的顶点C在函数y=  x的图象上,则实数m= .
x的图象上,则实数m= .
相关试题

