【题目】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)分别过![]() 、
、![]() 作平行直线
作平行直线![]() 、
、![]() ,若直线
,若直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,直线
无公共点,直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,其中点
两点,其中点![]() ,
, ![]() 在
在![]() 轴上方,求四边形
轴上方,求四边形![]() 的面积的取值范围.
的面积的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)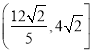 .
.
【解析】试题分析:(I)由焦距可得![]() ,故椭圆与抛物线交点坐标为
,故椭圆与抛物线交点坐标为![]() ,利用椭圆的定义求得
,利用椭圆的定义求得![]() ,利用
,利用![]() 解得
解得![]() ,由此求得椭圆的方程;(II)设出直线
,由此求得椭圆的方程;(II)设出直线![]() 的方程,联立直线的方程和抛物线的方程,利用判别式小于零求得
的方程,联立直线的方程和抛物线的方程,利用判别式小于零求得![]() 的取值范围.联立直线的方程和椭圆的方程,写出韦达定理,写出
的取值范围.联立直线的方程和椭圆的方程,写出韦达定理,写出![]() 的弦长,求得
的弦长,求得![]() 两条直线的距离,代入面积公式,化简后利用基本不等式求取值范围.
两条直线的距离,代入面积公式,化简后利用基本不等式求取值范围.
试题解析:
(Ⅰ)依题意得![]() ,则
,则![]() ,
, ![]() .
.
所以椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() ,
,
于是![]()
![]() ,从而
,从而![]() .
.
又![]() ,解得
,解得![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)依题意,直线![]() 的斜率不为0,设直线
的斜率不为0,设直线![]() :
: ![]() ,
,
由![]() ,消去
,消去![]() 整理得
整理得![]() ,由
,由![]() 得
得![]() .
.
由![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
![]()
![]() ,
,
![]() 与
与![]() 间的距离
间的距离![]() (即点
(即点![]() 到
到![]() 的距离),
的距离),
由椭圆的对称性知,四边形![]() 为平行四边形,
为平行四边形,
故![]()
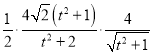
![]() ,
,
令![]() ,则
,则![]()
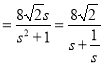
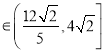 ,
,
所以四边形![]() 的面积的取值范围为
的面积的取值范围为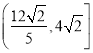 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
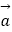 =(sin
=(sin 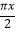 ,sin
,sin  ),
), 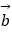 =(cos
=(cos 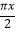 ,cos
,cos  ),且向量
),且向量 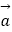 与向量
与向量 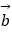 共线.
共线.
(1)求证:sin(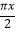 ﹣
﹣  )=0;
)=0;
(2)若记函数f(x)=sin(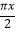 ﹣
﹣  ),求函数f(x)的对称轴方程;
),求函数f(x)的对称轴方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,满足f(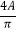 )=f(
)=f( 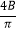 )=
)=  ,求
,求 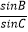 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=
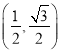 ,a与b不共线.
,a与b不共线.(1)求证:向量a+b与a-b垂直;
(2)当向量
 a+b与a-
a+b与a- b的模相等时,求α的大小.
b的模相等时,求α的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA = AB = 2,BC = 4, E是PD的中点,
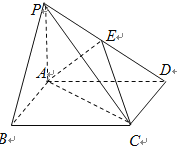
(1)求证:
 平面EAC;
平面EAC; (2)求证:平面PDC⊥平面PAD;
(3)求多面体
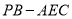 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
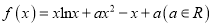 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.(1)求
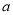 的取值范围.
的取值范围.(2)设
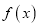 的两个极值点为
的两个极值点为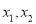 ,证明
,证明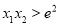
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 =
= 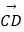 ,求D点的坐标;
,求D点的坐标;
(2)设向量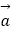 =
=  ,
, 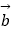 =
= 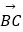 ,若k
,若k 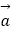 ﹣
﹣ 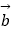 与
与 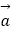 +3
+3 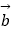 平行,求实数k的值.
平行,求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2cos2x+
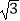 sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ,
,  ]时,求f(x)的值域.
]时,求f(x)的值域.
相关试题

