【题目】已知函数![]() 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.
(1)求![]() 的取值范围.
的取值范围.
(2)设![]() 的两个极值点为
的两个极值点为![]() ,证明
,证明![]()
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)极值点转化为导函数零点,即![]() 在
在![]() 有两个不同根.变量分离为
有两个不同根.变量分离为![]() ,利用导数可得函数
,利用导数可得函数![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增,根据趋势可得函数
上单调增,根据趋势可得函数![]() 在
在![]() 上范围为
上范围为![]() ,在
,在![]() 上范围为
上范围为![]() ,因此要有两解,需
,因此要有两解,需![]() ,(2)利用导数证明不等式关键是构造恰当的函数:
,(2)利用导数证明不等式关键是构造恰当的函数: ![]() 等价于
等价于![]()
![]() ,而由零点可得
,而由零点可得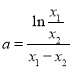 .代入化简得
.代入化简得![]() ,令
,令![]() ,则
,则![]() ,因此构造函数
,因此构造函数![]() ,利用导数求其最小值为
,利用导数求其最小值为![]() ,由于
,由于![]() ,所以命题得证.
,所以命题得证.
试题解析:(1)依题意,函数![]() 的定义域为
的定义域为![]() ,所以方程
,所以方程![]() 在
在![]() 有两个不同根.即方程
有两个不同根.即方程![]() 在
在![]() 有两个不同根.
有两个不同根.
转化为,函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点
上有两个不同交点
又![]() ,即
,即![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调增,在
上单调增,在![]() 上单调减,从而
上单调减,从而![]() .
.
又![]() 有且只有一个零点是1,且在
有且只有一个零点是1,且在![]() 时,
时, ![]() ,在
,在![]() 时,
时, ![]() ,
,
所以由![]() 的图象,要想函数
的图象,要想函数![]() 与函数
与函数![]() 的图象在
的图象在![]() 上有两个不同交点,只需
上有两个不同交点,只需![]() ,即
,即![]()
(2)由(1)可知![]() 分别是方程
分别是方程![]() 的两个根,即
的两个根,即![]() ,
, ![]() ,
,
设![]() ,作差得,
,作差得, ![]() ,即
,即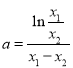 .
.
原不等式![]() 等价于
等价于
![]()
![]()
![]()
令![]() ,则
,则![]() ,
, ![]() ,
,
设![]() ,
, ![]() ,
, 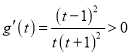 ,
,
∴函数![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,
,
即不等式![]() 成立,故所证不等式
成立,故所证不等式![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设在平面上有两个向量a=(cos 2α,sin 2α)(0≤α<π),b=
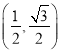 ,a与b不共线.
,a与b不共线.(1)求证:向量a+b与a-b垂直;
(2)当向量
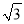 a+b与a-
a+b与a-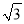 b的模相等时,求α的大小.
b的模相等时,求α的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA = AB = 2,BC = 4, E是PD的中点,
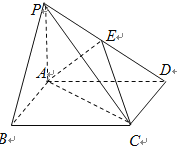
(1)求证:
 平面EAC;
平面EAC; (2)求证:平面PDC⊥平面PAD;
(3)求多面体
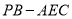 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
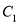 :
: 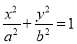 (
(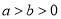 )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为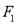 、
、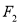 ,且
,且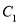 与抛物线
与抛物线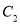 :
: 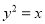 的交点所在的直线经过
的交点所在的直线经过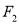 .
.(Ⅰ)求椭圆
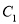 的方程;
的方程;(Ⅱ)分别过
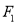 、
、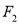 作平行直线
作平行直线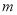 、
、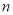 ,若直线
,若直线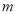 与
与 交于
交于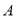 ,
, 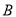 两点,与抛物线
两点,与抛物线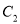 无公共点,直线
无公共点,直线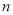 与
与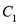 交于
交于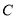 ,
, 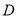 两点,其中点
两点,其中点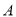 ,
, 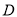 在
在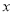 轴上方,求四边形
轴上方,求四边形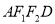 的面积的取值范围.
的面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 =
= 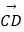 ,求D点的坐标;
,求D点的坐标;
(2)设向量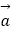 =
=  ,
, 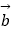 =
= 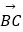 ,若k
,若k 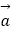 ﹣
﹣ 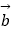 与
与 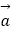 +3
+3 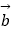 平行,求实数k的值.
平行,求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=2cos2x+
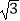 sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ,
,  ]时,求f(x)的值域.
]时,求f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:
 ,
, 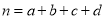 .
.
相关试题

