【题目】设函数f(x)=2cos2x+ ![]() sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
参考答案:
【答案】
(1)解:f(x)=2cos2x+ ![]() sin2x﹣1=cos2x+
sin2x﹣1=cos2x+ ![]() =
= ![]() ,
,
当2x+ ![]() ,即
,即 ![]() 时,f(x)max=2
时,f(x)max=2
(2)解:
(3)解:由 ![]() ,得
,得 ![]() ,
,
∴f(x)的单调减区间为[ ![]() ],k∈Z;
],k∈Z;
![]() ,
,
由 ![]() ,得
,得 ![]() ,
,
∴ ![]() ,
,
∴﹣1≤f(x)≤2.
则f(x)的值域为[﹣1,2]
【解析】f(x)=2cos2x+ ![]() sin2x﹣1=cos2x+
sin2x﹣1=cos2x+ ![]() (1)当2x+
(1)当2x+ ![]() ,即
,即 ![]() 时,f(x)取得最大值;(2)由
时,f(x)取得最大值;(2)由 ![]() ,得
,得 ![]() ,即可求出f(x)的单调减区间;(3)由
,即可求出f(x)的单调减区间;(3)由 ![]() ,得
,得 ![]() ,即可求出f(x)的值域.
,即可求出f(x)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
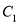 :
: 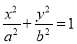 (
(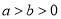 )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为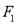 、
、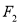 ,且
,且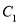 与抛物线
与抛物线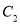 :
: 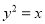 的交点所在的直线经过
的交点所在的直线经过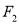 .
.(Ⅰ)求椭圆
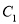 的方程;
的方程;(Ⅱ)分别过
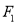 、
、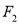 作平行直线
作平行直线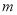 、
、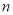 ,若直线
,若直线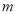 与
与 交于
交于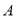 ,
, 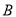 两点,与抛物线
两点,与抛物线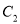 无公共点,直线
无公共点,直线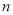 与
与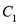 交于
交于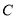 ,
, 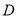 两点,其中点
两点,其中点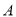 ,
, 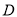 在
在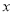 轴上方,求四边形
轴上方,求四边形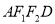 的面积的取值范围.
的面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
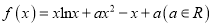 在其定义域内有两个不同的极值点.
在其定义域内有两个不同的极值点.(1)求
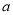 的取值范围.
的取值范围.(2)设
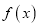 的两个极值点为
的两个极值点为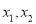 ,证明
,证明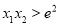
-
科目: 来源: 题型:
查看答案和解析>>【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,﹣2),C(4,1).
(1)若 =
= 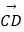 ,求D点的坐标;
,求D点的坐标;
(2)设向量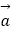 =
=  ,
, 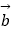 =
= 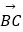 ,若k
,若k 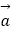 ﹣
﹣ 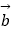 与
与 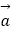 +3
+3 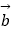 平行,求实数k的值.
平行,求实数k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:
 ,
, 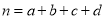 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,且
,且 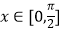 ,
,
(1)求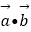 的取值范围;
的取值范围;
(2)求证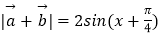 ;
;
(3)求函数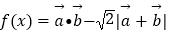 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,移动支付(又称手机支付)越来越普通,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有
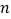 个人.把这
个人.把这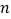 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组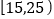 ,第2组
,第2组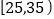 ,第3组
,第3组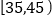 ,第4组
,第4组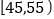 ,第5组
,第5组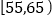 ,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图.其中,第一组的频数为20.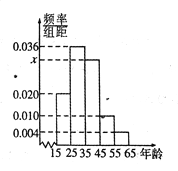
(1)求
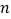 和
和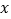 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
相关试题

