【题目】选修4-4:坐标系与参数方程
在直角坐标系中![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数,
为参数, ![]() ). 以坐标原点为极点,
). 以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动点,当
上的一个动点,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上所有的点均在直线
上所有的点均在直线![]() 的右下方,求
的右下方,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】【试题分析】(1)可先将直线的极坐标化为直角坐标方程,再借助曲线参数方程得到形式运用点到直线的距离公式建立目标函数,通过求函数的最值使得问题获解;(2)先将问题进行等价转化为不等式恒成立,然后再借助不等式恒成立建立不等式进行求解:
解:(1)由![]() ,得
,得![]() ,化成直角坐标方程,得
,化成直角坐标方程,得![]() ,即直线
,即直线![]() 的方程为
的方程为![]() ,依题意,设
,依题意,设![]() ,则
,则![]() 到直线
到直线![]() 的距离
的距离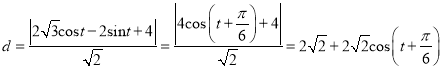 ,当
,当![]() ,即
,即![]() 时,
时, ![]() ,故点
,故点![]() 到直线
到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
(2)因为曲线![]() 上的所有点均在直线
上的所有点均在直线![]() 的右下方,
的右下方, ![]()
![]() ,
, ![]() 恒成立,即
恒成立,即
![]() (其中
(其中![]() )恒成立,
)恒成立, ![]() ,又
,又![]() ,解得
,解得![]() ,故
,故![]() 取值范围为
取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=
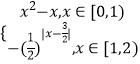 ,若x∈[﹣4,﹣2)时,f(x)≥
,若x∈[﹣4,﹣2)时,f(x)≥ 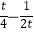 恒成立,则实数t的取值范围是( )
恒成立,则实数t的取值范围是( )
A.[﹣2,0)∪(0,1)
B.[﹣2,0)∪[1,+∞)
C.[﹣2,1]
D.(﹣∞,﹣2]∪(0,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为直角梯形,
为直角梯形,  ,
,  ,平面
,平面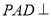 底面
底面 ,
,  为
为 的中点,
的中点,  是棱
是棱 上的点,
上的点,  ,
,  .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)若三棱锥
 的体积是四棱锥
的体积是四棱锥 体积的
体积的 ,设
,设 ,试确定
,试确定 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】由于某种商品开始收税,使其定价比原定价上涨x成(即上涨率为
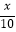 ),涨价后商品卖出的个数减少bx成,税率是新价的a成,这里a,b均为常数,且a<10,用A表示过去定价,B表示过去卖出的个数.
),涨价后商品卖出的个数减少bx成,税率是新价的a成,这里a,b均为常数,且a<10,用A表示过去定价,B表示过去卖出的个数.
(1)设售货款扣除税款后,剩余y元,求y关于x的函数解析式;
(2)要使y最大,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是(只填正确说法序号)
①若集合A={y|y=x﹣1},B={y|y=x2﹣1},则A∩B={(0,﹣1),(1,0)};
②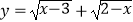 是函数解析式;
是函数解析式;
③ 是非奇非偶函数;
是非奇非偶函数;
④设二次函数f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),则f(x1+x2)=c. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|﹣1<x≤3},B={x|m≤x<1+3m}
(1)当m=1时,求A∪B;
(2)若BRA,求实数m的取值范围.
相关试题

