【题目】由于某种商品开始收税,使其定价比原定价上涨x成(即上涨率为 ![]() ),涨价后商品卖出的个数减少bx成,税率是新价的a成,这里a,b均为常数,且a<10,用A表示过去定价,B表示过去卖出的个数.
),涨价后商品卖出的个数减少bx成,税率是新价的a成,这里a,b均为常数,且a<10,用A表示过去定价,B表示过去卖出的个数.
(1)设售货款扣除税款后,剩余y元,求y关于x的函数解析式;
(2)要使y最大,求x的值.
参考答案:
【答案】
(1)解:定价上涨x成,即为A(1+ ![]() ),
),
卖出的个数为B(1﹣ ![]() ),售货款扣除税款后,
),售货款扣除税款后,
剩余y=AB(1+ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() ),(0<x<10)
),(0<x<10)
(2)解:y=AB(1+ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )
)
=AB(1﹣ ![]() )[﹣
)[﹣ ![]() +(
+( ![]() )x+1],
)x+1],
∴ ![]() ,
,
令y′=0,得x= ![]() ,
,
x∈(0, ![]() )时,y′>0;当x∈(
)时,y′>0;当x∈( ![]() )时,y′<0.
)时,y′<0.
∴ymax= ![]() =AB(1﹣
=AB(1﹣ ![]() )
) ![]() .
.
∴使y最大有x的值为 ![]()
【解析】(1)定价上涨x成,即为A(1+ ![]() ),卖出的个数为B(1﹣
),卖出的个数为B(1﹣ ![]() ),售货款扣除税款后,能求出y关于x的函数解析式.(2)由已知得
),售货款扣除税款后,能求出y关于x的函数解析式.(2)由已知得 ![]() ,由此利用导数性质能求出使y最大的x的值.
,由此利用导数性质能求出使y最大的x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.

(1)求证:A1B∥平面ADC1;
(2)求平面ADC1与ABA1所成二面角的平面角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,底面
中,底面 为直角梯形,
为直角梯形,  ,
,  ,平面
,平面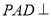 底面
底面 ,
,  为
为 的中点,
的中点,  是棱
是棱 上的点,
上的点,  ,
,  .
.
(Ⅰ)求证:平面
 平面
平面 ;
;(Ⅱ)若三棱锥
 的体积是四棱锥
的体积是四棱锥 体积的
体积的 ,设
,设 ,试确定
,试确定 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系中
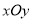 中,曲线
中,曲线 的参数方程为
的参数方程为 为参数,
为参数,  ). 以坐标原点为极点,
). 以坐标原点为极点,  轴正半轴为极轴建立极坐标系,已知直线
轴正半轴为极轴建立极坐标系,已知直线 的极坐标方程为
的极坐标方程为 .
.(1)设
 是曲线
是曲线 上的一个动点,当
上的一个动点,当 时,求点
时,求点 到直线
到直线 的距离的最大值;
的距离的最大值;(2)若曲线
 上所有的点均在直线
上所有的点均在直线 的右下方,求
的右下方,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是(只填正确说法序号)
①若集合A={y|y=x﹣1},B={y|y=x2﹣1},则A∩B={(0,﹣1),(1,0)};
②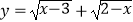 是函数解析式;
是函数解析式;
③ 是非奇非偶函数;
是非奇非偶函数;
④设二次函数f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),则f(x1+x2)=c. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A={x|﹣1<x≤3},B={x|m≤x<1+3m}
(1)当m=1时,求A∪B;
(2)若BRA,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(Ⅰ)当每辆车的月租金定为3600元时,能租出多少辆车?
(Ⅱ)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
相关试题

