【题目】设f(x)=log ![]()
![]() 为奇函数,a为常数,
为奇函数,a为常数,
(1)求a的值;
(2)证明f(x)在区间(1,+∞)上单调递增;
(3)若x∈[3,4],不等式f(x)>( ![]() )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:∵f(x)是奇函数,
∴f(﹣x)=﹣f(x),
∴ ![]() ,
,
∴ ![]() ,
,
即(1+ax)(1﹣ax)=﹣(x+1)(x﹣1),
即1﹣a2x2=1﹣x2,
即a2=1,
∴a=﹣1或a=1,
若a=1,则 ![]() =
= ![]() 不满足条件,舍去,
不满足条件,舍去,
故a=﹣1
(2)证明:∵ ![]() ,(x>1),
,(x>1),
设1<x1<x2,则△x=x2﹣x1>0
∵ ![]() ,
,
∴ ![]()
∴△y=f(x2)﹣f(x1)>0,f(x)在区间(1,+∞)上单调递增
(3)解:设 ![]() ,
,
则g(x)在[3,4]上是增函数
∴g(x)>m对x∈[3,4]恒成立,
∴m<g(3)=﹣ ![]()
【解析】(1)根据对数的基本运算以及函数奇偶性的性质建立条件关系即可求a的值;(2)根据函数单调性的定义即可证明f(x)在区间(1,+∞)上单调递增;(3)结合函数的单调性,利用参数分离法即可求出m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;(Ⅱ)证明:对于
 ,
,  在区间
在区间 上有极小值,且极小值大于0.
上有极小值,且极小值大于0. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用下图的两条线段表示;该商品在30天内日销售量Q(件)与时间t(天)之间的关系Q=﹣t+40.

(1)根据提供的图象,写出该商品每件的销售价格P与时间t的函数关系式;
(2)问这30天内,哪天的销售额最大,最大是多少?(销售额=销售价格×销售量) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
E是PC的中点.求证:

(Ⅰ)CD⊥AE;
(Ⅱ)PD⊥平面ABE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】奇函数f(x)、偶函数g(x)的图象分别如图1、2所示,方程f(g(x))=0、g(f(x))=0的实根个数分别为a、b,则a+b=( )

A.14
B.10
C.7
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在(﹣∞,+∞)上的偶函数,且在(﹣∞,0]上是增函数,设a=f(log47),b=f(log
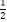 3),c=f(21.6),则a,b,c的大小关系是( )
3),c=f(21.6),则a,b,c的大小关系是( )
A.c<a<b
B.c<b<a
C.b<c<a
D.a<b<c -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
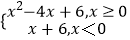 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )
A.(﹣3,1)∪(3,+∞)
B.(﹣3,1)∪(2,+∞)
C.(﹣1,1)∪(3,+∞)
D.(﹣∞,﹣3)∪(1,3)
相关试题

