【题目】(1)求与圆心在直线![]() 上,且过点A(2,-3),B(-2,-5)的圆C的方程.
上,且过点A(2,-3),B(-2,-5)的圆C的方程.
(2)设![]() 是圆C上的点,求
是圆C上的点,求![]() 的最大值和最小值.
的最大值和最小值.
参考答案:
【答案】(1) 圆C的方程为 (x+1)2+(y+2)2=10,(2) ![]() .
.
【解析】试题分析:(1)设圆的方程为x2+y2+Dx+Ey+F=0,代入A(2,﹣3),B(﹣2,﹣5),C(0,1),建立方程组,求出D,E,F,即可求出圆的方程;
(2)利用圆的参数方程求最值![]() ;
;
试题解析:(1)由于圆心在直线x﹣2y﹣3=0上,故可设圆C的圆心坐标为C(2a+3,a),
再由圆C经过A(2,﹣3)和B(﹣2,﹣5)两点,
可得|CA|=|CB|,∴|CA|2=|CB|2,
∴(2a+1)2+(a+3)2=(2a+5)2+(a+5)2.
解得a=﹣2,故圆心C(﹣1,﹣2),半径r=![]() ,
,
故圆C的方程为 (x+1)2+(y+2)2=10;
(2) ![]()
, ![]() ,
,
![]() ,
, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知坐标平面上点
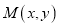 与两个定点
与两个定点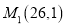 ,
, 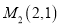 的距离之比等于5.
的距离之比等于5.(1)求点
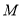 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;(2)记(1)中的轨迹为
 ,过点
,过点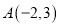 的直线
的直线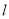 被
被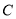 所截得的线段的长为 8,求直线
所截得的线段的长为 8,求直线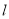 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),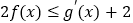 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
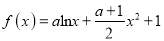 .
.(1)当
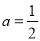 时,求
时,求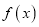 在区间
在区间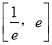 上的最值;
上的最值;(2)讨论函数
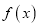 的单调性;
的单调性;(3)当
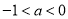 时,有
时,有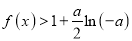 恒成立,求
恒成立,求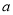 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
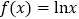 .
.(1)证明:
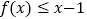 ;
;(2)若对任意
 ,不等式
,不等式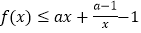 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
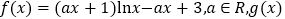 是
是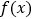 的导函数,
的导函数,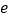 为自然对数的底数.
为自然对数的底数.(1)讨论
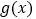 的单调性;
的单调性;(2)当
 时,证明:
时,证明: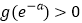 ;
;(3)当
 时,判断函数
时,判断函数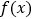 零点的个数,并说明理由.
零点的个数,并说明理由.
相关试题

