【题目】设函数f(x)=lg(ax﹣bx),且f(1)=lg2,f(2)=lg12
(1)求a,b的值.
(2)当x∈[1,2]时,求f(x)的最大值.
(3)m为何值时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
参考答案:
【答案】(1)a=4,b=2; (2)当x=2时,函数f(x)取最大值lg12,(3)![]()
【解析】试题分析:(1)根据条件得到关于a,b的方程组求解可得a=4,b=2;(2)由(1)得:函数f(x)=lg(4x﹣2x),根据x∈[1,2],可得![]() ,再由函数的单调性求最值;(3)设t=2x,将问题转化成方程
,再由函数的单调性求最值;(3)设t=2x,将问题转化成方程![]() 有两个正解处理,根据判别式和根与系数的关系可求解。
有两个正解处理,根据判别式和根与系数的关系可求解。
试题解析:(1)∵f(1)=lg2,f(2)=lg12, f(x)=lg(ax﹣bx)
∴![]() ,解得
,解得![]() 。
。
∴a=4,b=2;
(2)由(1)得:函数f(x)=lg(4x﹣2x),
当![]() 时,
时, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
故当![]() ,即x=2时,函数f(x)取最大值lg12。
,即x=2时,函数f(x)取最大值lg12。
(3)若函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点.
则方程4x﹣2x=m有两个解,
令t=2x,则t>0,
则方程![]() 有两个正解;
有两个正解;
故![]() , 解得
, 解得![]() 。
。
所以当![]() 时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点。
时,函数g(x)=ax的图象与h(x)=bx﹣m的图象恒有两个交点。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=xlnx,g(x)=x3+ax2-x+2.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)对任意x∈(0,+∞),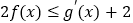 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
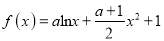 .
.(1)当
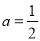 时,求
时,求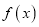 在区间
在区间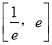 上的最值;
上的最值;(2)讨论函数
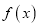 的单调性;
的单调性;(3)当
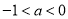 时,有
时,有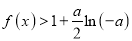 恒成立,求
恒成立,求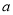 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求与圆心在直线
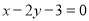 上,且过点A(2,-3),B(-2,-5)的圆C的方程.
上,且过点A(2,-3),B(-2,-5)的圆C的方程.(2)设
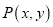 是圆C上的点,求
是圆C上的点,求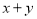 的最大值和最小值.
的最大值和最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
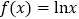 .
.(1)证明:
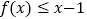 ;
;(2)若对任意
 ,不等式
,不等式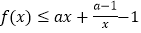 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
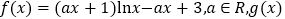 是
是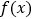 的导函数,
的导函数,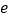 为自然对数的底数.
为自然对数的底数.(1)讨论
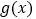 的单调性;
的单调性;(2)当
 时,证明:
时,证明: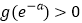 ;
;(3)当
 时,判断函数
时,判断函数 零点的个数,并说明理由.
零点的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男
女
总计
喜爱
40
60
100
不喜爱
20
20
40
总计
60
80
140
p(k2≥k0)
0.10
0.05
0.025
0.010
0.005
k0
2.705
3.841
5.024
6.635
7.879
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关?(精确到0.001)(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附:
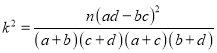
相关试题

