搜索
【题目】已知函数
．
（1）当
时，求
在
处的切线方程；
（2）设函数
，
（ⅰ）若函数
有且仅有一个零点时，求
的值；
（ⅱ）在（ⅰ）的条件下，若
，
，求
的取值范围。
参考答案：
【答案】（1）
（2）（ⅰ）
（ⅱ）
【解析】试题分析： （1）对函数
求导，求出
，即可求出切线方程；
（2）（ⅰ）分离参数得
，由函数
的单调性可知，
，可求得;（ⅱ）研究函数
的单调性，求出函数在区间
上的最大值即可.
试题解析：（1）当
时，
定义域
，
，又
在
处的切线方程4分
（2）（ⅰ）令
则
即
令，
则
令
，
，
在
上是减函数
又
所以当
时，
，当
时，
，
所以
在
上单调递增，在
上单调递减，
所以当函数
有且今有一个零点时，9分
（ⅱ）当，
，若
只需证明
令
得
或
又
，
函数在
上单调递增，在
上单调递减，在
上单调递增
又
，
即
13分
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
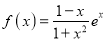若f（x1）=f（x2），且x1＜x2，关于下列命题：（1）f（x1）＞f（﹣x2）；（2）f（x2）＞f（﹣x1）；（3）f（x1）＞f（﹣x1）；（4）f（x2）＞f（﹣x2）．正确的个数为（ ）A. 1个 B. 2个 C. 3个 D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）计算27
+lg5﹣2log23+lg2+log29．
（2）已知f（x）=3x2﹣5x+2，求f（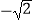
）、f（﹣a）、f（a+3）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知海岛A到海岸公路BC的距离AB=50km，B，C间的距离为100km，从A到C必须先坐船到BC上的某一点D，航速为25km/h，再乘汽车到C，车速为50km/h，记∠BDA=θ
（1）试将由A到C所用的时间t表示为θ的函数t（θ）；
（2）问θ为多少时，由A到C所用的时间t最少？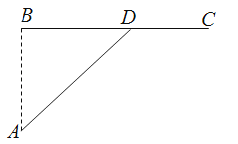
-
科目： 来源： 题型：
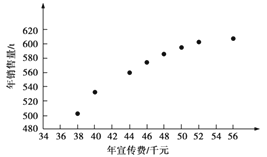
查看答案和解析>>【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x（单位:千元）对年销售量y（单位:t）和年利润z（单位:千元）的影响.对近8年的年宣传费xi和年销售量yi（i＝1,2,…,8）数据作了初步处理，得到下面的散点图及下面一些统计量的值.
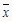
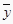
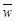
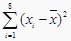
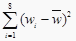
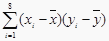
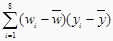
46.6
563
6.8
289.8
1.6
1469
108.8
表中
, 
.
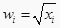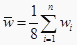附：对于一组数据（u1,v1）,（u2,v2）,…,（un,vn）,其回归直线v＝α＋βu的斜率和截距的最下二乘估计分别为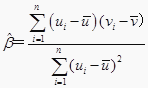
, 
.
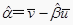（1）根据散点图判断,y＝a＋bx与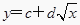
哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可,不必说明理由）
（2）根据（1）的判断结果及表中数据,建立y关于x的回归方程；
（3）已知这种产品的年利润z与x,y的关系为z＝0.2y－x.根据（2）的结果回答下列问题：
①年宣传费x＝49时,年销售量及年利润的预报值时多少？
②年宣传费x为何值时,年利润的预报值最大？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查，统计数据如下表所示：
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
参考公式及数据：
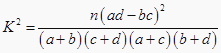
P（K2≥k）
0.050
0.010
0.001
k
3.841
6.635
10.828
（1）如果随机抽查这个班的一名学生，那么抽到积极参加班级工作的学生的概率是多少？抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少？
（2）试运用独立性检验的思想方法分析：学生的学习积极性与对待班级工作的态度是否有关系？并说明理由？ -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=ln（2+x），g（x）=ln（2﹣x）
（1）判断函数h（x）=f（x）﹣g（x）的奇偶性；
（2）求使f（x）≥g（x）成立的x的取值范围．
相关试题
