【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;
(3)已知在喜欢中国古典文学的10位男生中,![]() ,
,![]() ,
,![]() 还喜欢数学,
还喜欢数学,![]() ,
,![]() 还喜欢绘画,
还喜欢绘画,![]() ,
,![]() 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求![]() 和
和![]() 不全被选中的概率.
不全被选中的概率.
参考公式及数据:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】【试题分析】(1)依据题设条件,直接运用联列表分析求解;(2)借助题设条件,运用列联表的数据关系进行分析推断;(3)运用列举法及古典概型的计算公式分析求解:
(1)因为从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为![]() ,所以全班喜欢中国古典文学的学生为
,所以全班喜欢中国古典文学的学生为![]() 人,列联表补充如下:
人,列联表补充如下:
喜欢中国古典文学 | 不喜欢中国古典文学 | 合计 | |
女生 | 20 | 5 | 25 |
男生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(2)由列联表数据,得![]() ,
,
因为![]() ,所以有
,所以有![]() 的把握认为喜欢中国古典文学与性别有关.
的把握认为喜欢中国古典文学与性别有关.
(3)从喜欢数学、绘画和体育的男生中各选取1名,总的基本事件有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共12个,其中
共12个,其中![]() 和
和![]() 全被选中所包含的基本事件有
全被选中所包含的基本事件有![]() 、
、![]() 、
、![]() 共3个,则
共3个,则![]() 和
和![]() 不全被选中所包含的基本事件有9个.
不全被选中所包含的基本事件有9个.
于是![]() 和
和![]() 不全被选中的概率
不全被选中的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:
①线性回归方程
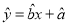 必过点
必过点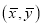 ;
;②在回归方程
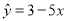 中,当变量
中,当变量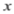 增加一个单位时,
增加一个单位时, 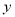 平均增加5个单位;
平均增加5个单位;③在回归分析中,相关指数
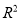 为0.80的模型比相关指数
为0.80的模型比相关指数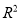 为0.98的模型拟合的效果要好;
为0.98的模型拟合的效果要好;④在回归直线
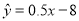 中,变量
中,变量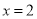 时,变量
时,变量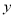 的值一定是-7.
的值一定是-7.其中假命题的个数是 ( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】宁夏某市2008年至2012年新建商品住宅每平方米的均价
 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:年份
2008
2009
2010
2011
2012
年份序号x
1
2
3
4
5
每平米均价y
2.0
3.1
4.5
6.5
7.9
(Ⅰ)求y关于x的线性回归方程
 ;
;(Ⅱ)利用(Ⅰ)中的回归方程,分析从2008年到2012年该市新建商品住宅每平方米均价的变化情况,并预测该市2015年新建商品住宅每平方米的均价.
附:回归直线的斜率和截距的最小二乘估计公式分别为
 ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,在三棱锥V-ABC中,VO⊥平面ABC,O∈CD,VA=VB,AD=BD,则下列结论中不一定成立的是 ( )
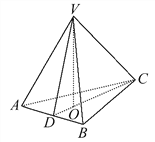
A. AC=BC
B. VC⊥VD
C. AB⊥VC
D. S△VCD·AB=S△ABC·VO
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批零件共160个,其中一级品有48人,二级品有64个,三级品有32个,等外品有16个.从中抽取一个容量为20的样本.试简要叙述用简单随机抽样、系统抽样、分层抽样法进行抽样都是等可能抽样.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值;
(2)求函数f(x)在
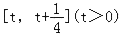 上的最小值;
上的最小值;(3)证明:对任意的x∈(0,+∞),都有
 成立
成立 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
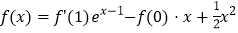 ,其中
,其中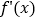 是函数
是函数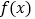 的导数.
的导数.(1)求
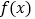 的单调区间;
的单调区间;(2)对于
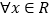 ,不等式
,不等式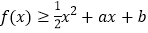 恒成立,求
恒成立,求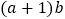 的最大值.
的最大值.
相关试题

