【题目】设函数![]() ,其中
,其中![]() 是函数
是函数![]() 的导数.
的导数.
(1)求![]() 的单调区间;
的单调区间;
(2)对于![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() ;(2)
;(2)![]() .
.
【解析】【试题分析】(1)依据题设条件,先对函数求导,再运用导数与函数的单调性之间的关系分析求解;(2)借助题设条件,运用等价转化的思想及分类整合思想建立函数关系,借助导数知识分析求解:
(1)对![]() 求导,得
求导,得![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,于是
,于是![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,于是
,于是![]() .
.
由![]() ,得
,得![]() .
.
令![]() ,显然
,显然![]() 是其一根.
是其一根.
又因为![]() 递增,所以
递增,所以![]() 只有唯一根
只有唯一根![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 递减;当
递减;当![]() 时,
时,![]() ,则
,则![]() 递增.
递增.
所以![]() 的递减区间为
的递减区间为![]() ,递增区间为
,递增区间为![]() .
.
(2)不等式![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
令![]() ,则只需
,则只需![]() .
.
由![]() ,得
,得![]() .
.
①当![]() ,即
,即![]() 时,
时,![]() ,则
,则![]() 在
在![]() 车上递增,没有最小值,舍去;
车上递增,没有最小值,舍去;
②当![]() ,即
,即![]() 时,令
时,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递减;
递减;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递增.
递增.
所以![]() .
.
于是只需![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]()
![]() ,由
,由![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递增;
递增;
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 递减.
递减.
所以![]() ,于是
,于是![]() ,即
,即![]() 的最大值为
的最大值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】高三(1)班班主任李老师为了了解本班学生喜爱中国古典文学是否与性别有关,对全班50人进行了问卷调查,得到如下列联表:
喜欢中国古典文学
不喜欢中国古典文学
合计
女生
5
男生
10
合计
50
已知从全班50人中随机抽取1人,抽到喜欢中国古典文学的学生的概率为
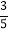 .
.(1)请将上面的列联表补充完整;
(2)是否有
 的把握认为喜欢中国古典文学与性别有关?请说明理由;
的把握认为喜欢中国古典文学与性别有关?请说明理由;(3)已知在喜欢中国古典文学的10位男生中,
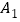 ,
, ,
, 还喜欢数学,
还喜欢数学,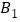 ,
,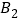 还喜欢绘画,
还喜欢绘画,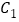 ,
,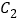 还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求
还喜欢体育.现从喜欢数学、绘画和体育的男生中各选出1名进行其他方面的调查,求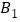 和
和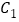 不全被选中的概率.
不全被选中的概率.参考公式及数据:
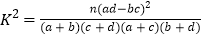 ,其中
,其中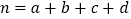 .
.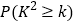
0.15
0.10
0.05
0.025
0.010
0.005
0.001
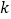
2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批零件共160个,其中一级品有48人,二级品有64个,三级品有32个,等外品有16个.从中抽取一个容量为20的样本.试简要叙述用简单随机抽样、系统抽样、分层抽样法进行抽样都是等可能抽样.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣2.
(1)若曲线f(x)=xlnx在x=1处的切线与函数g(x)=﹣x2+ax﹣2也相切,求实数a的值;
(2)求函数f(x)在
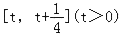 上的最小值;
上的最小值;(3)证明:对任意的x∈(0,+∞),都有
 成立
成立 -
科目: 来源: 题型:
查看答案和解析>>【题目】设正项数列
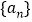 的前
的前 项和
项和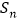 ,且满足
,且满足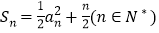 .
.(Ⅰ)计算
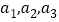 的值,猜想
的值,猜想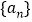 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;(Ⅱ)设
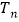 是数列
是数列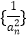 的前
的前 项和,证明:
项和,证明: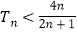 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平面
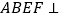 平面
平面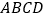 ,四边形
,四边形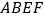 是正方形,四边形
是正方形,四边形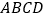 是菱形,且
是菱形,且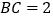 ,
,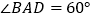 ,点
,点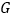 、
、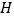 分别为边
分别为边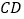 、
、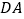 的中点,点
的中点,点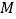 是线段
是线段 上的动点.
上的动点.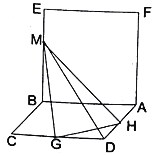
(1)求证:
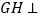
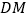 ;
;(2)求三棱锥
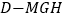 的体积的最大值.
的体积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
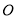 :
: 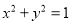 过椭圆
过椭圆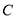 :
: 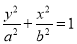 (
(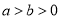 )的短轴端点,
)的短轴端点, 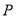 ,
, 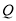 分别是圆
分别是圆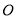 与椭圆
与椭圆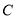 上任意两点,且线段
上任意两点,且线段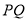 长度的最大值为3.
长度的最大值为3.(Ⅰ)求椭圆
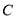 的方程;
的方程;(Ⅱ)过点
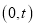 作圆
作圆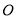 的一条切线交椭圆
的一条切线交椭圆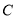 于
于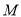 ,
, 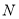 两点,求
两点,求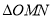 的面积的最大值.
的面积的最大值.
相关试题

