【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

参考答案:
【答案】32π
【解析】
设ED=a,根据勾股定理的逆定理可以通过计算可以证明出CE⊥ED. AM=x,根据三棱锥的体积公式,运用基本不等式,可以求出AM的长度,最后根据球的表面积公式进行求解即可.
设ED=a,则CD![]() a.可得CE2+DE2=CD2,∴CE⊥ED.
a.可得CE2+DE2=CD2,∴CE⊥ED.
当平面ABD⊥平面BCD时,当四面体C﹣EMN的体积才有可能取得最大值,设AM=x.
则四面体C﹣EMN的体积![]() (a﹣x)
(a﹣x)![]() a×x
a×x![]() ax(a﹣x)
ax(a﹣x)![]() ,当且仅当x
,当且仅当x![]() 时取等号.
时取等号.
解得a=2![]() .
.
此时三棱锥A﹣BCD的外接球的表面积=4πa2=32π.
故答案为:32π
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知直线
中,已知直线 的参数方程:
的参数方程: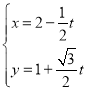 (
(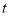 为参数),以原点为极点,
为参数),以原点为极点,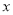 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆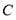 的极坐标方程为:
的极坐标方程为: .
.(1)将直线
 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆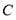 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;(2)求圆
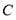 上的点到直线
上的点到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
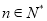 ,数列
,数列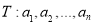 中的每一项均在集合
中的每一项均在集合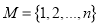 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数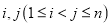 ,均有
,均有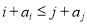 .例如
.例如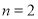 时,数列
时,数列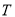 为
为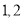 或
或 .
.(1)当
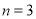 时,试求满足条件的数列
时,试求满足条件的数列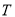 的个数;
的个数;(2)当
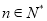 ,求所有满足条件的数列
,求所有满足条件的数列 的个数.
的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:
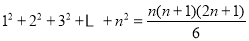 )
)A.1624B.1024C.1198D.1560
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早晩读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成如表:
考试分数
 ,
,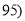
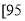 ,
,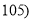
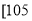 ,
,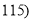
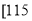 ,
,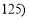
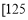 ,
,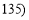
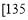 ,
,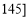
频数
5
10
15
5
10
5
赞成人数
4
6
9
3
6
4
(1)欲使测试优秀率为
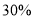 ,则优秀分数线应定为多少分?
,则优秀分数线应定为多少分?(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有
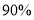 的把握认为赞成与否的态度与成绩是否优秀有关系.
的把握认为赞成与否的态度与成绩是否优秀有关系.参考公式及数据:
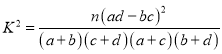 ,
,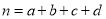 .
.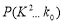
0.100
0.050
0.025
0.010
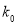
2.706
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
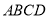 是正方形,点
是正方形,点 在以
在以 为直径的半圆弧上(
为直径的半圆弧上(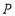 不与
不与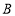 ,
,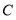 重合),
重合),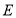 为线段
为线段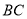 的中点,现将正方形
的中点,现将正方形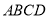 沿
沿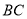 折起,使得平面
折起,使得平面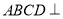 平面
平面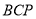 .
.
(1)证明:
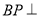 平面
平面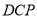 .
.(2)若
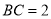 ,当三棱锥
,当三棱锥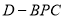 的体积最大时,求
的体积最大时,求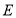 到平面
到平面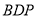 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
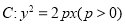 的焦点为
的焦点为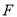 ,准线为
,准线为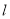 ,
,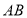 为过焦点
为过焦点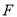 且垂直于
且垂直于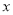 轴的抛物线
轴的抛物线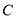 的弦,已知以
的弦,已知以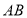 为直径的圆经过点
为直径的圆经过点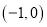 .
.(1)求
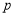 的值及该圆的方程;
的值及该圆的方程;(2)设
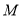 为
为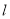 上任意一点,过点
上任意一点,过点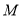 作
作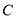 的切线,切点为
的切线,切点为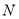 ,证明:
,证明: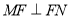 .
.
相关试题

