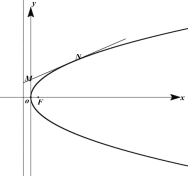
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 为过焦点
为过焦点![]() 且垂直于
且垂直于![]() 轴的抛物线
轴的抛物线![]() 的弦,已知以
的弦,已知以![]() 为直径的圆经过点
为直径的圆经过点![]() .
.
(1)求![]() 的值及该圆的方程;
的值及该圆的方程;
(2)设![]() 为
为![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 的切线,切点为
的切线,切点为![]() ,证明:
,证明:![]() .
.
参考答案:
【答案】(1)![]() ,圆的方程为:
,圆的方程为:![]() .(2)答案见解析
.(2)答案见解析
【解析】
(1)根据题意,可知![]() 点的坐标为
点的坐标为![]() ,即可求出
,即可求出![]() 的值,即可求出该圆的方程;
的值,即可求出该圆的方程;
(2)由题易知,直线![]() 的斜率存在且不为0,设
的斜率存在且不为0,设![]() 的方程为
的方程为![]() ,与抛物线
,与抛物线![]() 联立方程组,根据
联立方程组,根据![]() ,求得
,求得![]() ,化简解得
,化简解得![]() ,进而求得
,进而求得![]() 点的坐标为
点的坐标为![]() ,分别求出
,分别求出![]() ,
,![]() ,利用向量的数量积为0,即可证出
,利用向量的数量积为0,即可证出![]() .
.
解:(1)易知![]() 点的坐标为
点的坐标为![]() ,
,
所以![]() ,解得
,解得![]() .
.
又圆的圆心为![]() ,
,
所以圆的方程为![]() .
.
(2)证明易知,直线![]() 的斜率存在且不为0,
的斜率存在且不为0,
设![]() 的方程为
的方程为![]() ,
,
代入![]() 的方程,得
的方程,得![]() .
.
令![]() ,得
,得![]() ,
,
所以![]() ,解得
,解得![]() .
.
将![]() 代入
代入![]() 的方程,得
的方程,得![]() ,即
,即![]() 点的坐标为
点的坐标为![]() .
.
所以![]() ,
,![]() ,
,
![]() .
.
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD
 CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值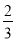 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早晩读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成如表:
考试分数
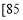 ,
,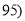
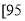 ,
,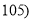
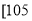 ,
,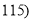
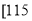 ,
,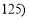
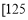 ,
,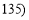
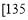 ,
,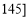
频数
5
10
15
5
10
5
赞成人数
4
6
9
3
6
4
(1)欲使测试优秀率为
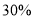 ,则优秀分数线应定为多少分?
,则优秀分数线应定为多少分?(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有
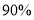 的把握认为赞成与否的态度与成绩是否优秀有关系.
的把握认为赞成与否的态度与成绩是否优秀有关系.参考公式及数据:
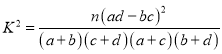 ,
,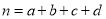 .
.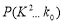
0.100
0.050
0.025
0.010
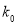
2.706
3.841
5.024
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
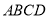 是正方形,点
是正方形,点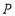 在以
在以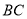 为直径的半圆弧上(
为直径的半圆弧上(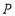 不与
不与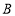 ,
,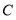 重合),
重合),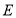 为线段
为线段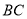 的中点,现将正方形
的中点,现将正方形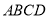 沿
沿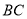 折起,使得平面
折起,使得平面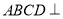 平面
平面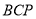 .
.
(1)证明:
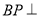 平面
平面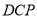 .
.(2)若
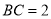 ,当三棱锥
,当三棱锥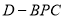 的体积最大时,求
的体积最大时,求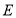 到平面
到平面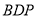 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
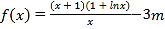 ,
,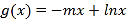
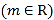 .
.(1)求函数
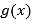 的单调区间与极值.
的单调区间与极值.(2)当
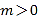 时,是否存在
时,是否存在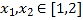 ,使得
,使得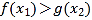 成立?若存在,求实数
成立?若存在,求实数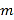 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
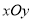 中,已知点
中,已知点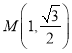 ,
,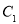 的参数方程为
的参数方程为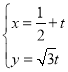 (
(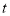 为参数),以坐标原点
为参数),以坐标原点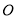 为极点,
为极点,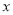 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线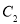 的极坐标方程为
的极坐标方程为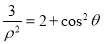 .
.(1)求
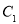 的普通方程和
的普通方程和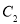 的直角坐标方程;
的直角坐标方程;(2)设曲线
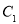 与曲线
与曲线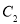 相交于
相交于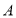 ,
,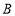 两点,求
两点,求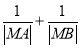 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】环境问题是当今世界共同关注的问题,我国环保总局根据空气污染指数
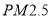 浓度,制定了空气质量标准:
浓度,制定了空气质量标准:空气污染质量
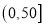
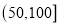
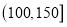
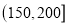
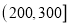
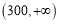
空气质量等级
优
良
轻度污染
中度污染
重度污染
严重污染
某市政府为了打造美丽城市,节能减排,从2010年开始考查了连续六年11月份的空气污染指数,绘制了频率分布直方图,经过分析研究,决定从2016年11月1日起在空气质量重度污染和严重污染的日子对机动车辆限号出行,即车牌尾号为单号的车辆单号出行,车牌尾号为双号的车辆双号出行(尾号为字母的,前13个视为单号,后13个视为双号).
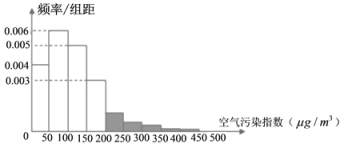
(1)某人计划11月份开车出行,求因空气污染被限号出行的概率;
(2)该市环保局为了调查汽车尾气排放对空气质量的影响,对限行三年来的11月份共90天的空气质量进行统计,其结果如表:
空气质量
优
良
轻度污染
中度污染
重度污染
严重污染
天数
16
39
18
10
5
2
根据限行前六年180天与限行后90天的数据,计算并填写
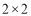 列联表,并回答是否有
列联表,并回答是否有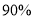 的把握认为空气质量的优良与汽车尾气的排放有关.
的把握认为空气质量的优良与汽车尾气的排放有关.空气质量优良
空气质量污染
合计
限行前
限行后
合计
参考数据:
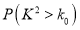
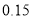

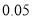
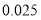
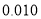
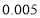
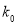
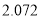
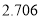
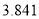
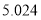
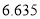
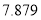
 其中
其中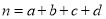
相关试题

