【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程:
的参数方程: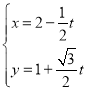 (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆
轴非负半轴为极轴(取相同单位长度)建立极坐标系,圆![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)求圆![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
参考答案:
【答案】(1)直线![]() 的普通方程为
的普通方程为![]() .圆
.圆![]() 的普通方程为
的普通方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据参数方程化普通方程方法、极坐标与直角坐标的互化原则可直接化简得到结果;
(2)设曲线![]() 上任一点
上任一点![]() ,利用点到直线距离公式可将问题转化为三角函数值域的求解问题,由正弦型函数性质可确定
,利用点到直线距离公式可将问题转化为三角函数值域的求解问题,由正弦型函数性质可确定![]() 时,
时,![]() 最小,进而得到结果.
最小,进而得到结果.
(1)直线![]() 的参数方程消去参数
的参数方程消去参数![]() 得普通方程为:
得普通方程为:![]() ;
;
由![]() 得:
得:![]() ,
,![]() ,
,
![]() 圆
圆![]() 的普通方程为
的普通方程为![]() ;
;
(2)在圆![]() 上任取一点
上任取一点![]() ,
,
则![]() 到直线
到直线![]() 的距离为
的距离为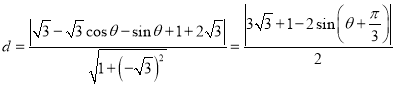
当![]() 时,
时,![]() ,此时
,此时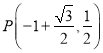 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,椭圆
中,椭圆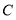 的方程为
的方程为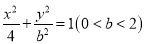 ,且直线
,且直线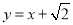 与以原点为圆心,椭圆
与以原点为圆心,椭圆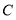 短轴长为直径的圆相切.
短轴长为直径的圆相切.(1)求
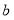 的值;
的值;(2)若椭圆
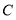 左右顶点分别为
左右顶点分别为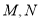 ,过点
,过点 作直线
作直线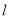 与椭圆交于
与椭圆交于 两点,且
两点,且 位于第一象限,
位于第一象限,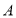 在线段
在线段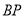 上.
上.①若
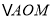 和
和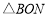 的面积分别为
的面积分别为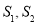 ,问是否存在这样的直线
,问是否存在这样的直线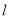 使得
使得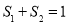 ?请说明理由;
?请说明理由;②直线
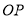 与直线
与直线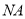 交于点
交于点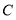 ,连结
,连结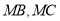 ,记直线
,记直线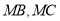 的斜率分别为
的斜率分别为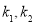 ,求证:
,求证: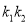 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
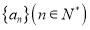 的前
的前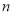 项和为
项和为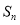 ,
,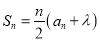 (
(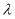 为常数)对于任意的
为常数)对于任意的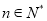 恒成立.
恒成立.(1)若
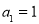 ,求
,求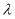 的值;
的值;(2)证明:数列
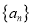 是等差数列;
是等差数列;(3)若
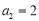 ,关于
,关于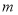 的不等式
的不等式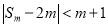 有且仅有两个不同的整数解,求
有且仅有两个不同的整数解,求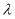 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
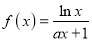 (
(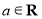 ,且
,且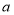 为常数).
为常数).(1)若函数
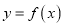 的图象在
的图象在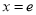 处的切线的斜率为
处的切线的斜率为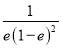 (
(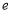 为自然对数的底数),求
为自然对数的底数),求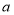 的值;
的值;(2)若函数
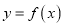 在区间
在区间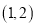 上单调递增,求
上单调递增,求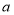 的取值范围;
的取值范围;(3)已知
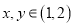 ,且
,且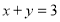 .求证:
.求证: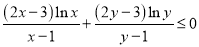 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
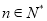 ,数列
,数列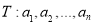 中的每一项均在集合
中的每一项均在集合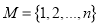 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数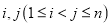 ,均有
,均有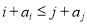 .例如
.例如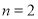 时,数列
时,数列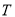 为
为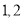 或
或 .
.(1)当
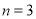 时,试求满足条件的数列
时,试求满足条件的数列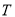 的个数;
的个数;(2)当
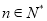 ,求所有满足条件的数列
,求所有满足条件的数列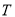 的个数.
的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为1,4,8,14,23,36,54,则该数列的第19项为( )(注:
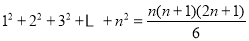 )
)A.1624B.1024C.1198D.1560
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD
 CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值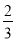 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.
相关试题

