【题目】如图,设椭圆C: ![]() (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(Ⅰ)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(Ⅱ)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
参考答案:
【答案】解:(Ⅰ)设直线l的方程为y=kx+m(k<0),由 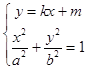 ,消去y得
,消去y得
(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0.
由于直线l与椭圆C只有一个公共点P,故△=0,即b2﹣m2+a2k2=0,
此时点P的横坐标为﹣ ![]() ,代入y=kx+m得
,代入y=kx+m得
点P的纵坐标为﹣k ![]() +m=
+m= ![]() ,
,
∴点P的坐标为(﹣ ![]() ,
, ![]() ),
),
又点P在第一象限,故m>0,
故m= ![]() ,
,
故点P的坐标为P( ![]() ,
, ![]() ).
).
(Ⅱ)由于直线l1过原点O且与直线l垂直,故直线l1的方程为x+ky=0,所以点P到直线l1的距离
d= 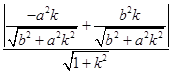 ,
,
整理得:d= 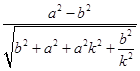 ,
,
因为a2k2+ ![]() ≥2ab,所以
≥2ab,所以 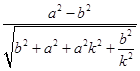 ≤
≤ ![]() =a﹣b,当且仅当k2=
=a﹣b,当且仅当k2= ![]() 时等号成立.
时等号成立.
所以,点P到直线l1的距离的最大值为a﹣b.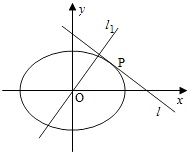
【解析】(Ⅰ)设直线l的方程为y=kx+m(k<0),由 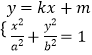 ,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,利用△=0,可求得在第一象限中点P的坐标;(Ⅱ)由于直线l1过原点O且与直线l垂直,设直线l1的方程为x+ky=0,利用点到直线间的距离公式,可求得点P到直线l1的距离d=
,消去y得(b2+a2k2)x2+2a2kmx+a2m2﹣a2b2=0,利用△=0,可求得在第一象限中点P的坐标;(Ⅱ)由于直线l1过原点O且与直线l垂直,设直线l1的方程为x+ky=0,利用点到直线间的距离公式,可求得点P到直线l1的距离d= 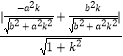 ,整理即可证得点P到直线l1的距离的最大值为a﹣b..
,整理即可证得点P到直线l1的距离的最大值为a﹣b..
-
科目: 来源: 题型:
查看答案和解析>>【题目】有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各个学校做问卷调查。某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分分别为;5, 8, 9, 9, 9:B班5名学生的得分分别为;6, 7, 8, 9, 10。
(1)请你分析A,B两个班中哪个班的问卷得分要稳定些;
(2)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若对所有x≥1都有f(x)≥ax﹣1,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设anbn= ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①第二象限角比第一象限角大;②设
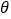 是第二象限角,则
是第二象限角,则 ;③三角形的内角是第一象限角或第二象限角;④函数
;③三角形的内角是第一象限角或第二象限角;④函数 是最小正周期为
是最小正周期为 的周期函数;⑤在△ABC中,若
的周期函数;⑤在△ABC中,若 ,则A>B.其中正确的是___________ (写出所有正确说法的序号)
,则A>B.其中正确的是___________ (写出所有正确说法的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a=(5
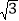 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+ .
.(1) 求函数f (x)的最小正周期和对称中心;
(2) 当
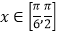 时,求函数f(x)的值域;
时,求函数f(x)的值域;(3) 该函数y=f (x)的图象可由
 的图象经过怎样的变换得到?
的图象经过怎样的变换得到? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 的焦点到准线的距离为
的焦点到准线的距离为 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,过这两点分别作抛物线
两点,过这两点分别作抛物线 的切线,且这两条切线相交于点
的切线,且这两条切线相交于点 .
.(1)若
 的坐标为
的坐标为 ,求
,求 的值;
的值;(2)设线段
 的中点为
的中点为 ,点
,点 的坐标为
的坐标为 ,过
,过 的直线
的直线 与线段
与线段 为直径的圆相切,切点为
为直径的圆相切,切点为 ,且直线
,且直线 与抛物线
与抛物线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围.
相关试题

