【题目】有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各个学校做问卷调查。某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分分别为;5, 8, 9, 9, 9:B班5名学生的得分分别为;6, 7, 8, 9, 10。
(1)请你分析A,B两个班中哪个班的问卷得分要稳定些;
(2)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取容量为2的样本,求样本平均数与总体平均数之差的绝对值不小于1的概率。
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)先求均值(一样),再求方差,选择方差较小的,(2)先确定总事件数,再确定样本平均数与总体平均数之差的绝对值不小于1的事件数,最后根据古典概型概率公式求结果.
详解:
(Ⅰ)∵![]() 班的
班的![]() 名学生的平均得分为
名学生的平均得分为![]()
![]() ÷
÷![]()
方差![]()
![]() 班的
班的![]() 名学生的平均得分为
名学生的平均得分为![]()
![]() ÷
÷![]()
方差![]()
∴![]()
![]() 且
且 ![]() ,
,
则![]() 班预防知识的问卷得分要稳定一些.
班预防知识的问卷得分要稳定一些.
(Ⅱ)从![]() 班
班![]() 名同学中任选
名同学中任选![]() 名同学的方法共有
名同学的方法共有![]() 种,
种,
其中样本![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() 的平均数满足条件,
的平均数满足条件,
故所求概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点.
(1)求证:|EA|+|EB|为定值;
(2)设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的函数f(x)满足:f′(x)﹣f(x)=xex , 且f(0)=
 ,则
,则 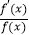 的最大值为( )
的最大值为( )
A.0
B.
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点.那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xlnx.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若对所有x≥1都有f(x)≥ax﹣1,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设anbn= ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设椭圆C:
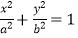 (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(Ⅰ)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(Ⅱ)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
相关试题

