【题目】设函数f(x)=log4(4x+1)+ax(a∈R).
(1)若函数f(x)是定义在R上的偶函数,求a的值;
(2)若不等式f(x)+f(﹣x)≥mt+m对任意x∈R,t∈[﹣2,1]恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:由函数f(x)是定义在R上的偶函数,得f(x)=f(﹣x)恒成立,
则 ![]() ,
,
∴ ![]() ,
,
∴(2a+1)x=0恒成立,则2a+1=0,故 ![]()
(2)解: ![]()
= ![]() .
.
当且仅当x=0时取等号,
∴mt+m≤1对任意t∈[﹣2,1]恒成立,
令h(t)=mt+m,
由 ![]() ,解得
,解得 ![]() ,
,
故实数m的取值范围是 ![]() .
.
【解析】(1)由偶函数的定义f(﹣x)=f(x)恒成立可求;(2)不等式f(x)+f(﹣x)≥mt+m对任意x∈R成立,等价于[f(x)+f(﹣x)]min≥mt+m,利用基本不等式可求得[f(x)+f(﹣x)]min , 然后构造关于t的一次函数,利用一次函数的性质可求得m范围.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣x2+ax﹣
 +
+  ,在区间[0,1]上的最大值是2,求函数f(x)在区间[0,1]上的最小值.
,在区间[0,1]上的最大值是2,求函数f(x)在区间[0,1]上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
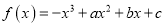 在
在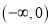 上是减函数,在
上是减函数,在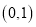 上是增函数,函数
上是增函数,函数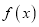 在
在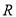 上有三个零点.
上有三个零点.(1)求
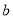 的值;
的值; (2)若1是其中一个零点,求
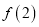 的取值范围;
的取值范围;(3)若
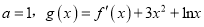 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由.
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为{x|x≠0},且满足对于定义域内任意的x1 , x2都有等式f(x1x2)=f(x1)+f(x2)成立.
(1)求f(1)的值.
(2)判断f(x)的奇偶性并证明.
(3)若f(4)=1,且f(x)在(0,+∞)上是增函数,解关于x的不等式f(3x+1)+f(﹣6)≤3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
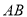 是圆
是圆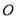 的直径,点
的直径,点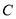 在圆
在圆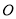 上,矩形
上,矩形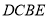 所在的平面垂直于圆
所在的平面垂直于圆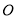 所在的平面,
所在的平面, 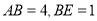 .
.
(1)证明:平面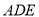 ⊥平面
⊥平面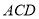 ;
;
(2)当三棱锥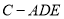 的体积最大时,求点
的体积最大时,求点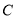 到平面
到平面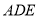 的距离.
的距离.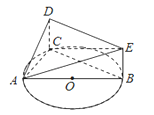
-
科目: 来源: 题型:
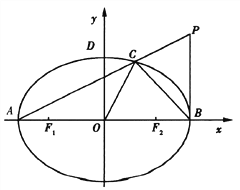
查看答案和解析>>【题目】已知椭圆
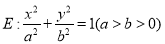 的左、右焦点分别为
的左、右焦点分别为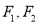 ,左、右顶点分别为
,左、右顶点分别为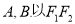 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为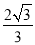 .设点
.设点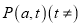 ,连接PA交椭圆于点C.
,连接PA交椭圆于点C.(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求t的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
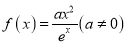 ,
, 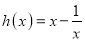 .
.(I)求函数
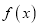 的单调区间;
的单调区间;(II)设
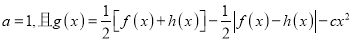 ,已知函数
,已知函数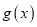 在
在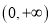 上是增函数.
上是增函数.(1)研究函数
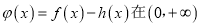 上零点的个数;
上零点的个数;(ii)求实数c的取值范围.
相关试题

