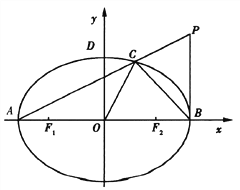
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,左、右顶点分别为
,左、右顶点分别为![]() 为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为
为直径的圆O过椭圆E的上顶点D,直线DB与圆O相交得到的弦长为![]() .设点
.设点![]() ,连接PA交椭圆于点C.
,连接PA交椭圆于点C.
(I)求椭圆E的方程;
(II)若三角形ABC的面积不大于四边形OBPC的面积,求t的最小值.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1) 由题意![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ,又
,又![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的弦长为
相交得到的弦长为![]() ,则
,则![]() 进而可得椭圆
进而可得椭圆![]() 的方程.(2) 设直线
的方程.(2) 设直线![]() 的方程为
的方程为![]() ,联立直线PA和椭圆方程,可得点
,联立直线PA和椭圆方程,可得点![]() 的坐标是
的坐标是![]() ,故直线
,故直线![]() 的斜率为
的斜率为![]() ,
, ![]()
![]() ,所以
,所以![]() .将线段BC,OP的长度用t来表示,则
.将线段BC,OP的长度用t来表示,则 ![]() ,
, ![]() ,所以
,所以![]() ,整理得
,整理得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() .
.
试题解析:(Ⅰ)因为以![]() 为直径的圆
为直径的圆![]() 过点
过点![]() ,所以
,所以![]() ,则圆
,则圆![]() 的方程为
的方程为![]() ,
,
又![]() ,所以
,所以![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 相交得到的
相交得到的
弦长为![]() ,则
,则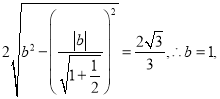 所以
所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设直线![]() 的方程为
的方程为![]() ,
,
由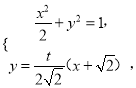
整理得![]() ,
,
解得: ![]() ,
, ![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,由于直线
,由于直线![]() 的斜率为
的斜率为![]() ,
,
所以![]()
![]() ,所以
,所以![]() .
.
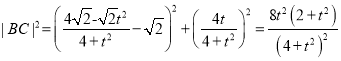 ,
, ![]() ,
,
所以![]() ,
,
![]() ,所以
,所以![]() ,
,
整理得![]() ,又
,又![]() ,
, ![]() ,所以
,所以![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为{x|x≠0},且满足对于定义域内任意的x1 , x2都有等式f(x1x2)=f(x1)+f(x2)成立.
(1)求f(1)的值.
(2)判断f(x)的奇偶性并证明.
(3)若f(4)=1,且f(x)在(0,+∞)上是增函数,解关于x的不等式f(3x+1)+f(﹣6)≤3. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=log4(4x+1)+ax(a∈R).
(1)若函数f(x)是定义在R上的偶函数,求a的值;
(2)若不等式f(x)+f(﹣x)≥mt+m对任意x∈R,t∈[﹣2,1]恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
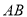 是圆
是圆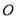 的直径,点
的直径,点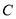 在圆
在圆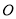 上,矩形
上,矩形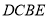 所在的平面垂直于圆
所在的平面垂直于圆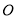 所在的平面,
所在的平面, 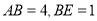 .
.
(1)证明:平面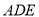 ⊥平面
⊥平面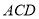 ;
;
(2)当三棱锥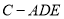 的体积最大时,求点
的体积最大时,求点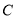 到平面
到平面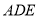 的距离.
的距离.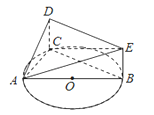
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
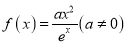 ,
, 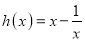 .
.(I)求函数
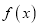 的单调区间;
的单调区间;(II)设
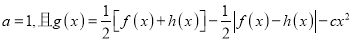 ,已知函数
,已知函数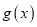 在
在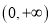 上是增函数.
上是增函数.(1)研究函数
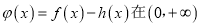 上零点的个数;
上零点的个数;(ii)求实数c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)求椭圆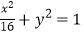 的长轴和短轴的长、离心率、焦点和顶点的坐标.
的长轴和短轴的长、离心率、焦点和顶点的坐标.
(2)求焦点在y轴上,焦距是4,且经过点M(3,2)的椭圆的标准方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设A={0,1,2,4},B={
 ,0,1,2,6,8},则下列对应关系能构成A到B的映射的是( )
,0,1,2,6,8},则下列对应关系能构成A到B的映射的是( )
A.f:x→x3﹣1
B.f:x→(x﹣1)2
C.f:x→2x﹣1
D.f:x→2x
相关试题

