【题目】如图,四边形![]() 是直角梯形,
是直角梯形, ![]() ,又
,又![]() ,直线
,直线![]() 与直线
与直线![]() 所成的角为
所成的角为![]() .
.

(1)求证: ![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析.(2)![]() .
.
【解析】试题分析:方法1:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)取BC的中点N,连MN.∵![]() ,∴
,∴![]() ,∴
,∴![]() 平面ABC.作
平面ABC.作![]()
![]() ,交AC的延长线于H,连结MH.由三垂线定理得
,交AC的延长线于H,连结MH.由三垂线定理得![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角.∵直线AM与直线PC所成的角为
的平面角.∵直线AM与直线PC所成的角为![]() ,∴在
,∴在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,
中, ![]() .
.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
故二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分
方法2:(1)∵![]() ,∴
,∴![]() 平面ABC,∴
平面ABC,∴![]() .5分
.5分
(2)在平面ABC内,过C作BC的垂线,并建立空间直角坐标系如图所示.设![]() ,则
,则![]() .
. 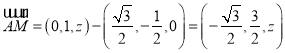 . 5分
. 5分
∵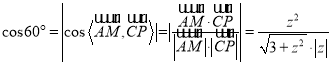 ,
,
且![]() ,∴
,∴![]() ,得
,得![]() ,∴
,∴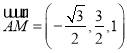 . 8分
. 8分
设平面MAC的一个法向量为![]() ,则由
,则由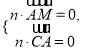 得
得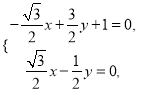 得
得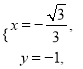 ∴
∴ . 10分
. 10分
平面ABC的一个法向量为![]() .
. 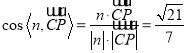 12分
12分
显然,二面角![]() 为锐二面角,∴二面角
为锐二面角,∴二面角![]() 的余弦值为
的余弦值为![]() .13分
.13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知常数
 ,向量
,向量 ,
,  ,经过点
,经过点 ,以
,以 为方向向量的直线与经过点
为方向向量的直线与经过点 ,以
,以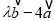 为方向向量的直线交于点
为方向向量的直线交于点 ,其中
,其中 .
.(
 )求点
)求点 的轨迹方程,并指出轨迹
的轨迹方程,并指出轨迹 .
.(
 )若点
)若点 ,当
,当 时,
时,  为轨迹
为轨迹 上任意一点,求
上任意一点,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,求曲线
时,求曲线 在点
在点 处的切线方程.
处的切线方程.(Ⅱ)当
 时,若曲线
时,若曲线 上的点
上的点 都在不等式组
都在不等式组 所表示的平面区域内,试求
所表示的平面区域内,试求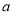 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的右焦点为
的右焦点为 ,右顶点为
,右顶点为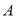 ,离心离为
,离心离为 ,点
,点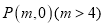 满足条件
满足条件 .
.(Ⅰ)求
 的值.
的值.(Ⅱ)设过点
 的直线
的直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,记
两点,记 和
和 的面积分别为
的面积分别为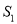 、
、 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知中心在原点,焦点在
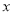 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为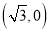 ,
, 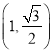 是椭圆上的一个点.
是椭圆上的一个点.(1)求椭圆的标准方程;
(2)设椭圆的上、下顶点分别为
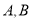 ,
, 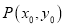 (
(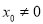 )是椭圆上异于
)是椭圆上异于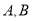 的任意一点,
的任意一点, 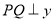 轴,
轴, 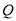 为垂足,
为垂足, 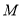 为线段
为线段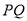 中点,直线
中点,直线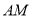 交直线
交直线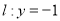 于点
于点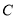 ,
, 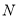 为线段
为线段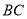 的中点,如果
的中点,如果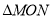 的面积为
的面积为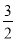 ,求
,求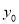 的值.
的值.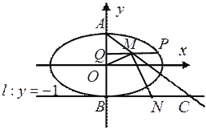
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,若存在
时,若存在 ,使得
,使得 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
 为正整数,方程
为正整数,方程 的两个实数根
的两个实数根 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入
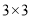 的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )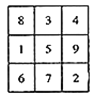
A. 9 B. 8 C. 6 D. 4
相关试题

