【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asinB= ![]() b.
b.
(1)求角A的大小;
(2)若a=6,b+c=8,求△ABC的面积.
参考答案:
【答案】
(1)解:由2asinB= ![]() b,利用正弦定理得:2sinAsinB=
b,利用正弦定理得:2sinAsinB= ![]() sinB,
sinB,
∵sinB≠0,∴sinA= ![]() ,
,
又A为锐角,
则A= ![]() ;
;
(2)解:由余弦定理得:a2=b2+c2﹣2bccosA,即36=b2+c2﹣bc=(b+c)2﹣3bc=64﹣3bc,
∴bc= ![]() ,又sinA=
,又sinA= ![]() ,
,
则S△ABC= ![]() bcsinA=
bcsinA= ![]() .
.
【解析】(1)利用正弦定理化简已知等式,求出sinA的值,由A为锐角,利用特殊角的三角函数值即可求出A的度数;(2)由余弦定理列出关系式,再利用完全平方公式变形,将a,b+c及cosA的值代入求出bc的值,再由sinA的值,利用三角形面积公式即可求出三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
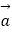 =(3,﹣1),
=(3,﹣1),  =(2,1) 求:
=(2,1) 求:
(1)|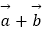 |.
|.
(2)求x的值使x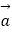 +3
+3  与3
与3 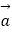 ﹣2
﹣2  为平行向量.
为平行向量. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列{an}的前n项和为Sn , 已知S1 , S3 , S2成等差数列,
(1)求{an}的公比q;
(2)求a1﹣a3=3,求Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4一5:不等式选讲.
已知函数
 .
.(1)求
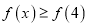 的解集;
的解集;(2)设函数
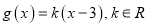 ,若
,若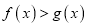 对任意的
对任意的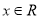 都成立,求实数
都成立,求实数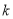 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=
 ,SA=SC=SD=2.
,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.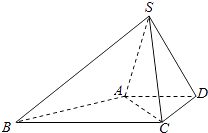
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C1的圆心在坐标原点O,且恰好与直线l1:x﹣2y+3
 =0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足
=0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足  ,设动点N的轨迹为曲线C.
,设动点N的轨迹为曲线C.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于不同两点A,B,且满足 (O为坐标原点),求线段AB长度的取值范围.
(O为坐标原点),求线段AB长度的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
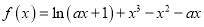 .
.(1)若
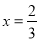 为
为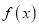 的极值点,求实数
的极值点,求实数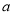 的值;
的值;(2)若
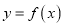 在
在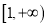 上为增函数,求实数
上为增函数,求实数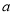 的取值范围;
的取值范围;(2)若
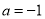 使方程
使方程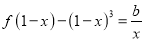 有实根,求实数
有实根,求实数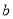 的取值范围.
的取值范围.
相关试题

