【题目】已知圆![]() 的方程:
的方程:![]()
(1)求m的取值范围;
(2)若圆C与直线![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)圆的方程要满足![]() ;或配成圆的标准方程,
;或配成圆的标准方程,![]() ;
;
(2) 利用弦心距公式,先求点到面的距离,利用![]() ,求出
,求出![]() 的值;
的值;
(3)设![]() ,若
,若![]() ,那么
,那么![]() ,利用直线方程与圆的方程联立,得到根与系数的关系式,代入后,求得
,利用直线方程与圆的方程联立,得到根与系数的关系式,代入后,求得![]() 的值.
的值.
试题解析:解:(1)(1)方程x2+y2-2x-4y+m=0,可化为
(x-1)2+(y-2)2=5-m,
∵此方程表示圆,
∴5-m>0,即m<5.
(2) 圆的方程化为 ![]() ,圆心 C(1,2),半径
,圆心 C(1,2),半径 ![]() ,
,
则圆心C(1,2)到直线![]() 的距离为
的距离为 
由于![]() ,则
,则![]() ,有
,有![]() ,
,
![]() 得
得![]() .
.
(3)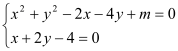
消去x得(4-2y)2+y2-2×(4-2y)-4y+m=0,
化简得5y2-16y+m+8=0.
设M(x1,y1),N(x2,y2),则
 ①②
①②
由OM⊥ON得y1y2+x1x2=0
即y1y2+(4-2y1)(4-2y2)=0,
∴16-8(y1+y2)+5y1y2=0.
将①②两式代入上式得
16-8×![]() +5×
+5×![]() =0,
=0,
解之得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
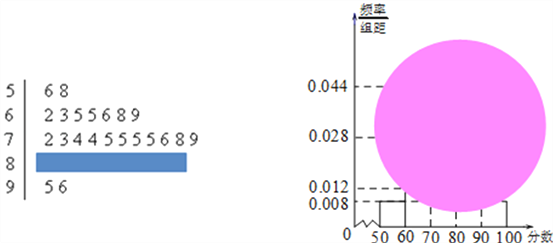
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是锐角三角形,cos22A+sin2A=1.
(Ⅰ)求角A;
(Ⅱ)若BC=1,B=x,求△ABC的周长f(x)的单调区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为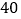 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为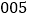 ,已知这
,已知这 名学生分住在三个营区,从
名学生分住在三个营区,从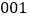 到
到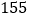 在第一营区,从
在第一营区,从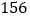 到
到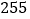 在第二营区,从
在第二营区,从 到
到 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
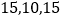 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力,经调查,得到关于这两种产品的有关数据如下表:
资金
每台产品所需资金(百元)
月资金供应量
(百元)
空调机
洗衣机
成本
30
20
300
劳动力(工资)
5
10
110
每台产品利润
6
8
试问:怎样确定两种货物的月供应量,才能使总利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
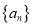 的奇数项是公差为
的奇数项是公差为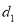 的等差数列,偶数项是公差为
的等差数列,偶数项是公差为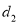 的等差数列,
的等差数列, 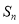 是数列
是数列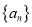 的前
的前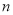 项和,
项和, 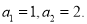
(1)若
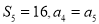 ,求
,求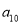 ;
;(2)已知
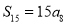 ,且对任意的
,且对任意的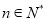 ,有
,有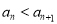 恒成立,求证:数列
恒成立,求证:数列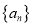 是等差数列;
是等差数列;(3)若
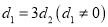 ,且存在正整数
,且存在正整数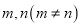 ,使得
,使得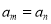 ,求当
,求当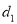 最大时,数列
最大时,数列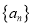 的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,
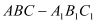 为三棱柱,且
为三棱柱,且 平面
平面 ,四边形
,四边形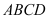 为平行四边形,
为平行四边形,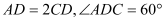 .
.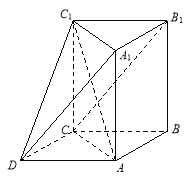
(1)若
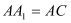 ,求证:
,求证: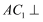 平面
平面 ;
;(2)若
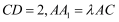 ,二面角
,二面角 的余弦值为
的余弦值为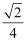 ,求三棱锥
,求三棱锥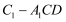 的体积.
的体积.
相关试题

