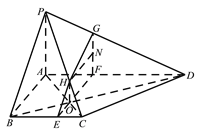
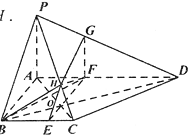
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角梯形,
为直角梯形,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,三棱锥
,三棱锥![]() 的体积为9.
的体积为9.

(1)求![]() 的值;
的值;
(2)过![]() 点的平面
点的平面![]() 平行于平面
平行于平面![]() ,
,![]() 与棱
与棱![]() ,
,![]() ,
,![]() ,
,![]() 分别相交于点
分别相交于点![]() ,求截面
,求截面![]() 的周长.
的周长.
参考答案:
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .
.
【解析】【试题分析】(1)利用体积公式列方程可求得![]() .(2)利用面面平行的性质定理可有
.(2)利用面面平行的性质定理可有![]() ,利用相似三角形可求得各边长,过点
,利用相似三角形可求得各边长,过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于
于![]() ,则
,则![]() .所以截面
.所以截面![]() 的周长为
的周长为![]() .
.
【试题解析】
(Ⅰ)四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,
![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,
所以![]() ,解得
,解得![]() .
.
(Ⅱ)【法一】因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,

平面![]() 平面
平面![]() ,
,
根据面面平行的性质定理,所以![]() ,
,
同理![]() , 因为
, 因为![]() ,
,
所以![]() ∽
∽![]() ,且
,且![]() ,
,
又因为![]() ∽
∽![]() ,
,![]() ,所以
,所以![]() ,
,
同理![]() ,
,![]() ,
,
![]()
如图:作![]() ,所以
,所以![]() ,
,
故四边形![]() 为矩形,即
为矩形,即![]() , (求
, (求![]() 长2分,其余三边各1分)
长2分,其余三边各1分)
在![]() 中,所以
中,所以![]()
所以截面![]() 的周长为
的周长为![]() .
.
【法二】因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,同理
,同理![]()
因为![]() ∥
∥![]()
所以![]() ∽
∽![]() ,且
,且![]() ,
,
所以![]() ,
,![]()
同理![]() ,连接
,连接![]() ,则有
,则有![]() ∥
∥![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() ,同理,
,同理,![]() ,
,
过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于
于![]() ,则
,则![]() ,
,
所以截面![]() 的周长为
的周长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,
中,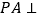 底面
底面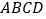 ,
,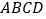 为直角梯形,
为直角梯形,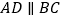 ,
,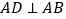 ,
,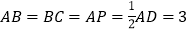 ,
,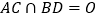 ,过
,过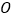 点作平面
点作平面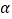 平行于平面
平行于平面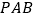 ,平面
,平面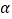 与棱
与棱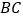 ,
,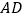 ,
,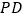 ,
,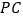 分别相交于点
分别相交于点 ,
,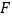 ,
,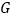 ,
,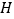 .
.
(1)求
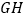 的长度;
的长度;(2)求二面角
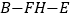 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在
 ,按照区间
,按照区间 ,
, ,
, ,
, ,
, 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
完成表格,并判断是否有
 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
(2)从乙班
 ,
, ,
, 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自 发言的人数为随机变量
发言的人数为随机变量 ,求
,求 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数再取整,绘制成如下茎叶图,规定不低于85分(百分制)为优秀,甲班同学成绩的中位数为74.


(1)求
 的值和乙班同学成绩的众数;
的值和乙班同学成绩的众数;(2)完成表格,若有
 以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
以上的把握认为“数学成绩优秀与教学改革有关”的话,那么学校将扩大教学改革面,请问学校是否要扩大改革面?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的下顶点为
的下顶点为 ,右顶点为
,右顶点为 ,离心率
,离心率 ,抛物线
,抛物线 的焦点为
的焦点为 ,
, 是抛物线
是抛物线 上一点,抛物线
上一点,抛物线 在点
在点 处的切线为
处的切线为 ,且
,且 .
.(1)求直线
 的方程;
的方程;(2)若
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,且
两点,且 ,求
,求 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 为自然对数的底数.
为自然对数的底数.(1)若
 在
在 处取到极小值,求
处取到极小值,求 的值及函数
的值及函数 的单调区间;
的单调区间;(2)若当
 时,
时,
 恒成立,求
恒成立,求 的取值范围.
的取值范围.
相关试题

