【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]() 有实数根,求实数
有实数根,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)当
;(2)当![]() 时,方程
时,方程![]() 有实数根.
有实数根.
【解析】试题分析:(1)函数求导![]() ,从而得单调区间;
,从而得单调区间;
(2)方程![]() 有实数根,即函数
有实数根,即函数![]() 存在零点,分类讨论函数
存在零点,分类讨论函数![]() 的单调性,从而得有零点时参数的范围.
的单调性,从而得有零点时参数的范围.
试题解析:
(1)依题意,得![]()
![]() ,
,![]() .
.
令![]() ,即
,即![]() .
.
解得![]() ;
;
令![]() ,即
,即![]() .
.
解得![]() .
.
故函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)由题得,![]()
![]() .
.
依题意,方程![]() 有实数根,
有实数根,
即函数![]() 存在零点.
存在零点.
又![]() .
.
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() .
.
即函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
而![]() ,
,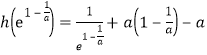
![]() .
.
所以函数![]() 存在零点;
存在零点;
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:

所以![]() 为函数
为函数![]() 的极小值,也是最小值.
的极小值,也是最小值.
当![]() ,即
,即![]() 时,函数
时,函数![]() 没有零点;
没有零点;
当![]() ,即
,即![]() 时,注意到
时,注意到![]() ,
,
![]() ,
,
所以函数![]() 存在零点.
存在零点.
综上所述,当![]() 时,方程
时,方程![]() 有实数根.
有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是函数y=f(x)的导函数f′(x)的图象,则下面判断正确的是( )

A.在区间(﹣2,1)上f(x)是增函数
B.在(1,3)上f(x)是减函数
C.在(4,5)上f(x)是增函数
D.当x=4时,f(x)取极大值 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知0<a<1,f(x)=ax , g(x)=logax,h(x)=
 ,当x>1时,则有( )
,当x>1时,则有( )
A.f(x)<g(x)<h(x)
B.g(x)<f(x)<h(x)
C.g(x)<h(x)<f(x)
D.h(x)<g(x)<f(x) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|log0.5x|,若正实数m,n(m<n)满足f(m)=f(n),且f(x)在区间[m2 , n]上的最大值为4,则n﹣m=( )
A.
B.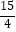
C.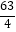
D.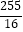
-
科目: 来源: 题型:
查看答案和解析>>【题目】直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=
 ,M是CC1的中点,则异面直线AB1与A1M所成角为 .
,M是CC1的中点,则异面直线AB1与A1M所成角为 .
相关试题

