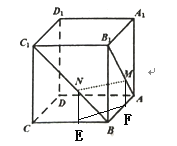
【题目】棱长为1的正方体![]() 中,点
中,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上运动(不包括线段端点),且
上运动(不包括线段端点),且![]() .以下结论:①
.以下结论:①![]() ;②若点
;②若点![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,则由线
的中点,则由线![]() 与
与![]() 确定的平面在正方体
确定的平面在正方体![]() 上的截面为等边三角形;③四面体
上的截面为等边三角形;③四面体![]() 的体积的最大值为
的体积的最大值为![]() ;④直线
;④直线![]() 与直线
与直线![]() 的夹角为定值.其中正确的结论为______.(填序号)
的夹角为定值.其中正确的结论为______.(填序号)

参考答案:
【答案】① ② ③
【解析】
①作NE⊥BC,MF⊥AB,垂足分别为E,F,可得四边形MNEF是矩形,可得MN∥FE,利用AA1⊥面AC,可得结论成立;
②截面为△AB1C,为等边三角形,故正确.
③设![]()
![]() ,则
,则![]() =
=![]() dM﹣BCN=
dM﹣BCN=![]() ,故③成立;
,故③成立;
④设![]()
![]() ,当
,当![]() 接近于0时,直线
接近于0时,直线![]() 与直线
与直线![]() 的夹角接近于
的夹角接近于![]() ,当
,当![]() 接近于1时,夹角接近于
接近于1时,夹角接近于![]() ,故④不正确;
,故④不正确;
①作NE⊥BC,MF⊥AB,垂足分别为E,F,∵AM=BN,∴NE=MF,∴四边形MNEF是矩形,∴MN∥FE,∵AA1⊥面AC,EF面AC,∴AA1⊥EF,∴AA1⊥MN,故①正确;
②点M、N分别为线段AB1、BC1的中点,则由线MN与AB1确定的平面在正方体ABCD﹣A1B1C1D1 上的截面为△AB1C,为等边三角形,故②正确.
③设![]()
![]() ,则
,则![]() =
=![]() dM﹣BCN,又AM=BN=
dM﹣BCN,又AM=BN=![]() ,
,
∴![]() =
=![]() ,dM﹣BCN =
,dM﹣BCN =![]() ,∴
,∴![]() =
=![]() dM﹣BCN=
dM﹣BCN=![]() ,当且仅当
,当且仅当![]() 时取得最大值,故③成立;
时取得最大值,故③成立;
④设![]()
![]() ,当
,当![]() 接近于0时,直线
接近于0时,直线![]() 与直线
与直线![]() 的夹角近似于直线
的夹角近似于直线![]() 和直线
和直线![]() 的夹角,接近于
的夹角,接近于![]() ,当
,当![]() 接近于1时,直线
接近于1时,直线![]() 与直线
与直线![]() 的夹角近似于直线
的夹角近似于直线![]() 和直线
和直线![]() 的夹角,接近于
的夹角,接近于![]() ,故④不正确;
,故④不正确;
综上可知,正确的结论为①②③
故答案为:①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于
 的方程
的方程 有一个实数解,则实数
有一个实数解,则实数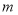 的取值范围是______.
的取值范围是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:  过点
过点 ,且两个焦点的坐标分别为
,且两个焦点的坐标分别为 ,
,  .
.(1)求
 的方程;
的方程;(2)若
 ,
,  ,
, 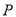 为
为 上的三个不同的点,
上的三个不同的点,  为坐标原点,且
为坐标原点,且 ,求证:四边形
,求证:四边形 的面积为定值.
的面积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
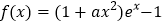 .
.(1)若
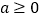 时,讨论函数
时,讨论函数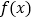 的单调性;
的单调性;(2)若函数
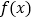 在区间
在区间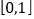 上恰有2个零点,求实数
上恰有2个零点,求实数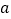 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ,且
,且 ).
).(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)求函数
 在
在 上的最大值.
上的最大值.【答案】(Ⅰ)
 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 .(Ⅱ)当
.(Ⅱ)当 时,
时, 
 ;当
;当 时,
时, 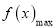
 .
.【解析】【试题分析】(I)利用
 的二阶导数来研究求得函数
的二阶导数来研究求得函数 的单调区间.(II) 由(Ⅰ)得
的单调区间.(II) 由(Ⅰ)得 在
在 上单调递减,在
上单调递减,在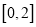 上单调递增,由此可知
上单调递增,由此可知 .利用导数和对
.利用导数和对 分类讨论求得函数在
分类讨论求得函数在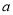 不同取值时的最大值.
不同取值时的最大值.【试题解析】
(Ⅰ)
 ,
,设

 ,则
,则 .
.∵
 ,
,  ,∴
,∴ 在
在 上单调递增,
上单调递增,从而得
 在
在 上单调递增,又∵
上单调递增,又∵ ,
,∴当
 时,
时,  ,当
,当 时,
时,  ,
,因此,
 的单调增区间为
的单调增区间为 ,单调减区间为
,单调减区间为 .
.(Ⅱ)由(Ⅰ)得
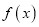 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,由此可知
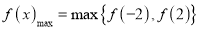 .
.∵
 ,
,  ,
,∴
 .
.设
 ,
,则


 .
.∵当
 时,
时,  ,∴
,∴ 在
在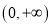 上单调递增.
上单调递增.又∵
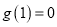 ,∴当
,∴当 时,
时,  ;当
;当 时,
时,  .
.①当
 时,
时,  ,即
,即 ,这时,
,这时, 
 ;
;②当
 时,
时,  ,即
,即 ,这时,
,这时, 
 .
.综上,
 在
在 上的最大值为:当
上的最大值为:当 时,
时, 
 ;
;当
 时,
时, 
 .
.[点睛]本小题主要考查函数的单调性,考查利用导数求最大值. 与函数零点有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与
 轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.
轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.【题型】解答题
【结束】
22【题目】选修4-4:坐标系与参数方程
在直角坐标系
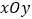 中,圆
中,圆 的普通方程为
的普通方程为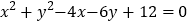 . 在以坐标原点为极点,
. 在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线 的极坐标方程为
的极坐标方程为 .
.(Ⅰ) 写出圆
 的参数方程和直线
的参数方程和直线 的直角坐标方程;
的直角坐标方程;( Ⅱ ) 设直线
 与
与 轴和
轴和 轴的交点分别为
轴的交点分别为 ,
, 为圆
为圆 上的任意一点,求
上的任意一点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,将圆
中,将圆 上每一点的横坐标保持不变,纵坐标变为原来的
上每一点的横坐标保持不变,纵坐标变为原来的 倍,再把所得曲线上每一点向下平移1个单位得到曲线
倍,再把所得曲线上每一点向下平移1个单位得到曲线 .以
.以 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是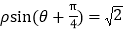 .
.(1)写出
 的参数方程和
的参数方程和 的直角坐标方程;
的直角坐标方程;(2)设点
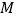 在
在 上,点
上,点 在
在 上,求使
上,求使 取最小值时点
取最小值时点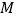 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)讨论
 的单调性;
的单调性;(2)若存在正数
 ,使得当
,使得当 时,
时, ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

