【题目】已知抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() :
:![]() 的一个顶点重合,且这个顶点与椭圆
的一个顶点重合,且这个顶点与椭圆![]() 的两个焦点构成的三角形面积为
的两个焦点构成的三角形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的上顶点为
的上顶点为![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,连接
为坐标原点,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)根据抛物线的性质可得椭圆中的![]() ,再根据三角形的面积求出
,再根据三角形的面积求出![]() ,根据
,根据![]() ,即可求出椭圆方程,
,即可求出椭圆方程,
(Ⅱ)过点![]() 的直线方程为
的直线方程为![]() ,代入到由
,代入到由![]() 得
得![]() ,可求出
,可求出![]() 点的坐标,再求出
点的坐标,再求出![]() 的坐标和
的坐标和![]() 的坐标,以及|
的坐标,以及|![]() 和点
和点![]() 到直线
到直线![]() 的距离,根据三角形的面积求出
的距离,根据三角形的面积求出![]() 的值.
的值.
详解:
(1)因为抛物线![]() 的焦点
的焦点![]() 与椭圆
与椭圆![]() 的一个顶点重合,∴
的一个顶点重合,∴![]() ,
,
又椭圆![]() 的顶点与其两个焦点构成的三角形的面积为
的顶点与其两个焦点构成的三角形的面积为![]() ,
,
∴![]() ,
,![]()
∴![]()
故椭圆的方程是![]() .
.
(2)由题意设直线![]() 的方程为
的方程为![]() ,设点
,设点![]()
由![]() 得
得![]()
解得![]()
∴![]() ,
,
∴![]()
直线![]() 斜率
斜率 ,直线
,直线![]() 的方程为
的方程为![]() ,
,
由 得
得![]()
点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为

![]()
∵![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]()
令![]() ,则
,则![]() ,解得
,解得![]()
![]() ,∴
,∴![]() ,解得
,解得![]() 或
或![]() (舍)
(舍)
∴![]() 的值为
的值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图1是由矩形
 和菱形
和菱形 组成的一个平面图形,其中
组成的一个平面图形,其中 ,
,  ,将其沿
,将其沿 折起使得
折起使得 与
与 重合,连结
重合,连结 ,如图2.
,如图2.(1)证明图2中的
 四点共面,且平面
四点共面,且平面 平面
平面 ;
;(2)求图2中的四边形
 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在空间中,给出下列说法:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面
 内有不共线的三点到平面
内有不共线的三点到平面 的距离相等,则
的距离相等,则 ;④过平面
;④过平面 的一条斜线,有且只有一个平面与平面
的一条斜线,有且只有一个平面与平面 垂直.其中正确的是( )
垂直.其中正确的是( )A. ①③B. ②④C. ①④D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行评分,评分的频数分布表如下:
女性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
20
40
80
50
10
男性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
45
75
90
60
30
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);

(2)把评分不低于70分的用户称为“评分良好用户”,能否有
 的把握认为“评分良好用户”与性别有关?
的把握认为“评分良好用户”与性别有关?参考附表:










参考公式
 ,其中
,其中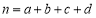
-
科目: 来源: 题型:
查看答案和解析>>【题目】某制造商3月生产了一批乒乓球,从中随机抽样100个进行检查,测得每个球的直径(单位:mm),将数据分组如下:
分组
频数
频率
[39.95,39.97)
10
[39. 97,39.99)
20
[39.99,40.01)
50
[40.01,40.03]
20
合计
100

(Ⅰ)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图;
(Ⅱ)若以上述频率作为概率,已知标准乒乓球的直径为40.00 mm,试求这批球的直径误差不超过0.03 mm的概率;
(Ⅲ)统计方法中,同一组数据经常用该组区间的中点值(例如区间[39.99,40.01)的中点值是40.00作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
相关试题

