【题目】假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的线性回归方程,对于基本苗数56.7预报其有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求R2,并说明残差变量对有效穗的影响占百分之几.
参考答案:
【答案】(1)见解析 (2)![]() =0.29x+34.708,估计成熟期有效穗51.151. (3)
=0.29x+34.708,估计成熟期有效穗51.151. (3) ![]() =0.342,
=0.342, ![]() =0.773 8,
=0.773 8, ![]() =-0.508,
=-0.508, ![]() =-2.222,
=-2.222, ![]() =1.616.
=1.616. ![]() =8.521 30.(4) R2=0.830,残差变量贡献了约1-83%=17%.
=8.521 30.(4) R2=0.830,残差变量贡献了约1-83%=17%.
【解析】试题分析:(1)建立坐标系根据各组值点出每个点即可(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系,根据表中数据,计算![]() ,
, ![]() 与
与![]() 写出线性回归方程,代入x=56.7时即得解(3)由于y=bx+a+e,可以算得
写出线性回归方程,代入x=56.7时即得解(3)由于y=bx+a+e,可以算得![]() =yi-
=yi-![]() 分别为
分别为![]() =0.342,
=0.342, ![]() =0.773 8,
=0.773 8, ![]() =-0.508,
=-0.508, ![]() =-2.222,
=-2.222, ![]() =1.616.进行求和即得总残差平方和(4)计算总偏差平方和,回归平方和=总偏差平方和-残差平方和,代入公式得R2,解释变量小麦基本苗数对总效应贡献即得,残差变量贡献即得.
=1.616.进行求和即得总残差平方和(4)计算总偏差平方和,回归平方和=总偏差平方和-残差平方和,代入公式得R2,解释变量小麦基本苗数对总效应贡献即得,残差变量贡献即得.
试题解析:
(1)如下图所示:
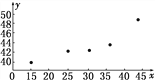
(2)由图看出,样本点呈条状分布,有比较好的线性相关关系,因此可以用线性回归方程刻画它们之间的关系.设回归方程为![]() =
=![]() x+
x+![]() ,
,![]() =30.316,
=30.316,![]() =43.5,
=43.5,![]() =5 090.256 4,
=5 090.256 4,
![]()
![]() =1 318.746,
=1 318.746,![]() 2=1 892.25,
2=1 892.25,![]() 2=919.059 9,
2=919.059 9,
![]() iyi=6 737.322.
iyi=6 737.322.
则![]() =
=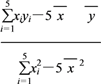 ≈0.29.
≈0.29.![]() =
=![]() -
-![]()
![]() ≈34.708.
≈34.708.
故所求的线性回归方程为![]() =0.29x+34.708.
=0.29x+34.708.
当x=56.7时,![]() =0.29×56.7+34.708=51.151,估计成熟期有效穗51.151.
=0.29×56.7+34.708=51.151,估计成熟期有效穗51.151.
(3)由于y=bx+a+e,可以算得![]() i=yi-
i=yi-![]() i分别为
i分别为![]() =0.342,
=0.342, ![]() =0.773 8,
=0.773 8, ![]() =-0.508,
=-0.508, ![]() =-2.222,
=-2.222, ![]() =1.616.
=1.616.
残差平方和:![]() =8.521 30.
=8.521 30.
(4)总偏差平方和:![]() (yi-
(yi-![]() )2=50.18,
)2=50.18,
回归平方和:50.18-8.521 30=41.658 7,
R2=0.830.
∴解释变量小麦基本苗数对总效应贡献了约83%.
残差变量贡献了约1-83%=17%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 ,且椭圆上任意一点到左焦点的最大距离为
,且椭圆上任意一点到左焦点的最大距离为 ,最小距离为
,最小距离为 .
.(1)求椭圆的方程;
(2)过点
 的动直线
的动直线 交椭圆
交椭圆 于
于 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点 ,使得以线段
,使得以线段 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出点
?若存在,求出点 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
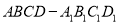 中,
中, 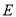 是棱
是棱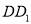 的中点.
的中点.(
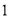 )求直线
)求直线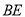 和平面
和平面 所成角的正弦值.
所成角的正弦值.(
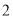 )在棱
)在棱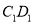 上是否存在一点
上是否存在一点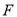 ,使
,使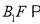 平面
平面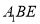 ?证明你的结论.
?证明你的结论.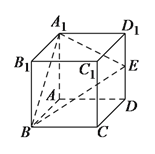
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
(1)若用分层抽样的方法从“优秀警员”和“优秀陪练员”中共提取10人,然后再从这10人中选4人,那么至少有1人是“优秀警员”的概率是多少?
(2)若所有“优秀警员”中选3名代表,用
 表示所选女“优秀警员”的人数,试求
表示所选女“优秀警员”的人数,试求 的分布列和数学期望.
的分布列和数学期望.
-
科目: 来源: 题型:
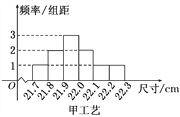
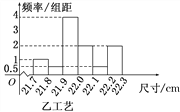
查看答案和解析>>【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)∪[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示.
P(K2≥k0)
0.10
0.05
0.01
k0
2.706
3.841
6.635
附:
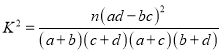
(1)根据上述数据完成下列2×2列联表,根据此数据,你认为选择不同的工艺与生产出一等品是否有关?
甲工艺
乙工艺
总计
一等品
非一等品
总计
(2)以上述各种产品的频率作为各种产品发生的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(x个月)和市场占有率(y%)的几组相关对应数据:
x
1
2
3
4
5
y
0.02
0.05
0.1
0.15
0.18
(1)根据上表中的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过0.5%(精确到月).
附:
 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有两个分类变量x与y,其一组观测值如下面的2×2列联表所示:
y1
y2
x1
a
20-a
x2
15-a
30+a
其中a,15-a均为大于5的整数,则a取何值时,在犯错误的概率不超过0.1的前提下认为x与y之间有关系?
相关试题

