【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
参考答案:
【答案】(1)![]() (
(![]() 且
且![]() 为正整数);(2)当售价定为每件
为正整数);(2)当售价定为每件![]() 或
或![]() 元,每个月的利润最大,最大的月利润是
元,每个月的利润最大,最大的月利润是![]() 元.
元.
【解析】试题分析:(1)首先计算每一件的利润=售价-成本=![]() ,每月生产
,每月生产![]() 件,然后相乘就是
件,然后相乘就是![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)将函数整理为关于![]() 的二次函数,并且配方,根据定义域求函数的最大值,主要定义域.
的二次函数,并且配方,根据定义域求函数的最大值,主要定义域.
试题解析:解:(1)依题意可得每件商品的售价上涨![]() 元(
元(![]() 为正整数),
为正整数),
则每件商品对应的利润为![]() 元,而对应的销售量为
元,而对应的销售量为![]() ,
,
所以每个月的销售利润为![]() ,其中
,其中![]() 为正整数且
为正整数且![]() .
.
(2)由![]()
可得利润![]() 是关于
是关于![]() 的一元二次函数
的一元二次函数
开口向下且对称轴为![]() ,所以当
,所以当![]() 取
取![]() 时,
时,
即每件商品的售价定为![]() 元或
元或![]() 元时,每个月的利润最大,最大利润为
元时,每个月的利润最大,最大利润为![]() 元
元
-
科目: 来源: 题型:
查看答案和解析>>【题目】空气质量指数(
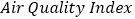 ,简称
,简称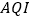 )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为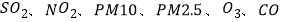 等六项.空气质量按照
等六项.空气质量按照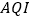 大小分为六级:一级
大小分为六级:一级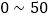 为优;二级
为优;二级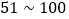 为良好;三级
为良好;三级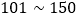 为轻度污染;四级
为轻度污染;四级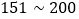 为中度污染;五级
为中度污染;五级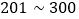 为重度污染;六级
为重度污染;六级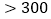 为严重污染.
为严重污染.某人根据环境监测总站公布的数据记录了某地某月连续10天
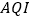 的茎叶图如图所示:
的茎叶图如图所示:
(1)利用访样本估计该地本月空气质量优良(
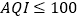 )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);(2)若从样本中的空气质量不佳(
 )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径
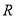
,此时圆内接正六边形的周长为
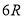
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据:
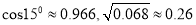
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
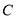 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在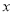 轴上,焦点到短轴端点的距离为2,离心率为
轴上,焦点到短轴端点的距离为2,离心率为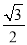 .
.(Ⅰ)求该椭圆的方程;
(Ⅱ)若直线
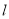 与椭圆
与椭圆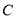 交于
交于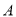 ,
, 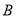 两点且
两点且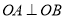 ,是否存在以原点
,是否存在以原点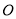 为圆心的定圆与直线
为圆心的定圆与直线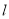 相切?若存在求出定圆的方程;若不存在,请说明理由
相切?若存在求出定圆的方程;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员
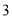 名,其中种子选手
名,其中种子选手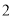 名;乙协会的运动员
名;乙协会的运动员 名,其中种子选手
名,其中种子选手 名.从这
名.从这 名运动员中随机选择
名运动员中随机选择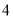 人参加比赛.
人参加比赛.(1)设
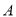 为事件“选出的
为事件“选出的 人中恰有
人中恰有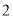 名种子选手,且这
名种子选手,且这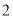 名种子选手来自同一个协会”求事件
名种子选手来自同一个协会”求事件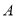 发生的概率;
发生的概率;(2)设
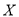 为选出的
为选出的 人中种子选手的人数,求随机变量
人中种子选手的人数,求随机变量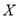 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1时,f(x)=x2.如果函数g(x)=f(x)-(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z) B.2k或2k+
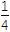 (k∈Z)
(k∈Z)C.0 D.2k或2k-
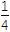 (k∈Z)
(k∈Z) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
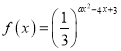 .
.(1)若
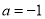 ,求
,求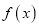 的单调区间;
的单调区间;(2)若
 有最大值
有最大值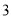 ,求
,求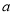 的值.
的值.
相关试题

