【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论方程![]() 根的个数.
根的个数.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时,方程
时,方程![]() 有一个根,当
有一个根,当![]() 时,方程
时,方程![]() 有三个根.
有三个根.
【解析】
试题分析:(1)![]() 时,函数表达式已知,先求出切点的坐标,利用导数求得斜率,用点斜式写出切线方程;(2)方程
时,函数表达式已知,先求出切点的坐标,利用导数求得斜率,用点斜式写出切线方程;(2)方程![]() 即
即![]() ,
,![]() 的定义域为
的定义域为![]() .当
.当![]() 时,易知
时,易知![]() ,故方程
,故方程![]() 无解,故只需考虑
无解,故只需考虑![]() 的情况.此时构造函数
的情况.此时构造函数![]() ,利用导数分类讨论
,利用导数分类讨论![]() 的零点个数.
的零点个数.
试题解析:
(1)当![]() 时,
时,![]() 又
又![]()
![]() 故所求切线方程为;
故所求切线方程为;![]()
(2) 方程![]() 即
即![]() ,
,![]() 的定义域为
的定义域为![]()
当![]() 时,易知
时,易知![]() ,故方程
,故方程![]() 无解,故只需考虑
无解,故只需考虑![]() 的情况
的情况
设![]() ,令
,令![]() 得
得![]() ,又
,又![]()
当![]() 时,
时,![]() 所以
所以![]() 在区间
在区间![]() 上是增函数,又
上是增函数,又![]() ,只有一个根0
,只有一个根0
当![]() 时,由
时,由![]() 得
得![]()
又![]() ,所以
,所以![]() 在
在![]() 和
和![]() 递增,在
递增,在![]() 递减
递减
![]() ,
,![]() 在
在![]() 递减
递减![]()
又![]() 在
在![]() 递增,
递增,![]() 在
在![]() 有一个根
有一个根
![]() 在
在![]() 递减
递减![]()
![]() 在
在![]() 有一个根0
有一个根0
![]() ,又
,又![]() 在
在![]() 递增
递增
![]() 在
在![]() 有一个根
有一个根
综上所述,当![]() 时方程
时方程![]() 有一个根,当
有一个根,当![]() 时方程
时方程![]() 有三个根.
有三个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
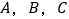 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).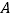 班
班6
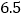
7
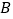 班
班6
7
8
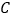 班
班5
6
7
8
(1)试估计
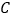 班学生人数;
班学生人数;(2)从
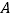 班和
班和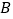 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记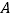 班选出的学生为甲,
班选出的学生为甲,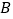 班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,求甲的锻炼时间大于乙的锻炼时间的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
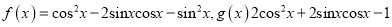 把
把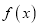 的图象向右平移
的图象向右平移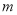 个单位后,图象恰好为函数
个单位后,图象恰好为函数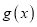 的图象,则
的图象,则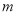 的值可以是( )
的值可以是( )A.
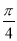 B.
B. 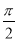 C.
C. 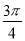 D.
D. 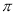
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车厂生产
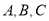 三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有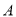 类轿车10辆.
类轿车10辆.
(1)求
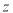 的值;
的值;(2)用分层抽样的方法在
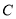 类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;(3)用随机抽样的方法从
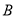 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
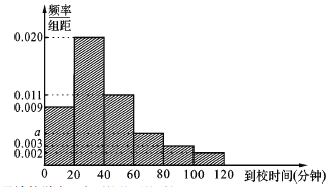
(1)求
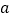 的值及该校学生从家到校的平均时间;
的值及该校学生从家到校的平均时间;(2)若该校因学生寝室不足,只能容纳全校
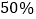 的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4,
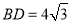 ,AB=2CD=8.
,AB=2CD=8.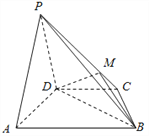
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
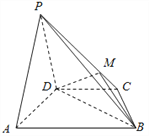
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
相关试题

