【题目】已知函数![]() ,曲线
,曲线![]() 在
在![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() .
.
(1)求![]() 的值;
的值;
(2)若对于![]() 内的任意两个数
内的任意两个数![]() ,
,![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)求出原函数的导函数,得到f′(1),求出f(1),可得切线方程,代入(0,![]() )即可求得m值;
)即可求得m值;
(2)把(1)中求得的m值代入函数解析式,设x1>x2,把对于(1,+∞)内的任意两个数x1,x2,![]() a(x1+x2)转化为
a(x1+x2)转化为![]() ,设g(x)=f(x)﹣ax2,则g(x)=x2lnx
,设g(x)=f(x)﹣ax2,则g(x)=x2lnx![]() x3+x﹣ax2 在(1,+∞)上为减函数,可得g′(x)=2xlnx+x﹣x2+1﹣2ax≤0对x>1恒成立,分离参数a,再由导数求最值得答案.
x3+x﹣ax2 在(1,+∞)上为减函数,可得g′(x)=2xlnx+x﹣x2+1﹣2ax≤0对x>1恒成立,分离参数a,再由导数求最值得答案.
解:(1)由![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
∴曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
则![]() ,解得
,解得![]() ;
;
(2)![]() ,
,
不妨设![]() ,对于
,对于![]() 内的任意两个数
内的任意两个数![]() ,
,![]() ,
,![]() ,
,
即有![]() ,
,
设![]() ,则
,则![]() 在
在![]() 上为减函数.
上为减函数.
则![]() 对
对![]() 恒成立.
恒成立.
可得![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,![]() ,
,
则![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
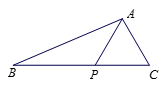
查看答案和解析>>【题目】如图, 在△
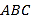 中, 点
中, 点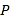 在
在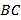 边上,
边上, 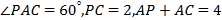 .
.(Ⅰ)求
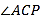 ;
;(Ⅱ)若△
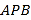 的面积是
的面积是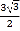 , 求
, 求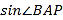 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 +
+ =1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2
=1(a>b>0)上的点P到左,右两焦点F1,F2的距离之和为2 ,离心率为
,离心率为 .
.(1)求椭圆的标准方程;
(2)过右焦点F2的直线l交椭圆于A,B两点,若y轴上一点M(0,
 )满足|MA|=|MB|,求直线l的斜率k的值.
)满足|MA|=|MB|,求直线l的斜率k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,A,B,C三点满足
 。
。(1)求证:A,B,C三点共线;
(2)若A(1,cosx),B(1+sinx,cosx),且x∈[0,
 ],函数f(x)=
],函数f(x)= (2m+
(2m+ )|
)| |+m2的最小值为5,求实数m的值。
|+m2的最小值为5,求实数m的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】A4纸是生活中最常用的纸规格.A系列的纸张规格特色在于:①A0、A1、A2…、A5,所有尺寸的纸张长宽比都相同.②在A系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张A0纸对裁后可以得到2张A1纸,1张A1纸对裁可以得到2张A2纸,依此类推.这是因为A系列纸张的长宽比为
 :1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈
:1这一特殊比例,所以具备这种特性.已知A0纸规格为84.1厘米×118.9厘米.118.9÷84.1≈1.41≈ ,那么A4纸的长度为( )
,那么A4纸的长度为( )A.
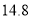 厘米B.
厘米B. 厘米C.
厘米C.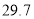 厘米D.
厘米D.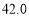 厘米
厘米 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C于A,B两点,圆M是以线段AB为直径的圆.
(1)证明:坐标原点O在圆M上;
(2)设圆M过点P(4,-2),求直线l与圆M的方程.
【答案】(1)见解析;(2)

【解析】(1)证明略;(2)直线
 的方程为
的方程为 ,圆
,圆 的方程为
的方程为 .或直线
.或直线 的方程为
的方程为 ,圆
,圆 的方程为
的方程为
试题分析:(1)设出点的坐标,联立直线与抛物线的方程,由斜率之积为
 可得
可得 ,即得结论;(2)结合(1)的结论求得实数
,即得结论;(2)结合(1)的结论求得实数 的值,分类讨论即可求得直线
的值,分类讨论即可求得直线 的方程和圆
的方程和圆 的方程.
的方程.试题解析:(1)设
 ,
, .
.由
 可得
可得 ,则
,则 .
.又
 ,故
,故 .
.因此
 的斜率与
的斜率与 的斜率之积为
的斜率之积为 ,所以
,所以 .
.故坐标原点
 在圆
在圆 上.
上.(2)由(1)可得
 .
.故圆心
 的坐标为
的坐标为 ,圆
,圆 的半径
的半径 .
.由于圆
 过点
过点 ,因此
,因此 ,故
,故 ,
,即
 ,
,由(1)可得
 .
.所以
 ,解得
,解得 或
或 .
.当
 时,直线
时,直线 的方程为
的方程为 ,圆心
,圆心 的坐标为
的坐标为 ,圆
,圆 的半径为
的半径为 ,圆
,圆 的方程为
的方程为 .
.当
 时,直线
时,直线 的方程为
的方程为 ,圆心
,圆心 的坐标为
的坐标为 ,圆
,圆 的半径为
的半径为 ,圆
,圆 的方程为
的方程为 .
.【名师点睛】直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系;在解决直线与抛物线的位置关系时,要特别注意直线与抛物线的对称轴平行的特殊情况.中点弦问题,可以利用“点差法”,但不要忘记验证
 或说明中点在曲线内部.
或说明中点在曲线内部.【题型】解答题
【结束】
21【题目】已知函数
 .
.(1)若
 ,求a的值;
,求a的值;(2)设m为整数,且对于任意正整数n,
 ,求m的最小值.
,求m的最小值.
相关试题

