【题目】四边形![]() 的顶点
的顶点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为坐标原点.
为坐标原点.
(![]() )此四边形是否有外接圆,若有,求出外接圆的方程;若没有,请说明理由.
)此四边形是否有外接圆,若有,求出外接圆的方程;若没有,请说明理由.
(![]() )记
)记![]() 的外接圆为
的外接圆为![]() ,过
,过![]() 上的点
上的点![]() 作圆
作圆![]() 的切线
的切线![]() ,设与
,设与![]() 轴、
轴、![]() 轴的正半轴分别交于点
轴的正半轴分别交于点![]() 、
、![]() ,求
,求![]() 面积的最小值.
面积的最小值.
参考答案:
【答案】(![]() )外接圆方程为
)外接圆方程为![]() (
(![]() )
)![]()
【解析】试题分析:
(1)先求出过![]() 三点的圆,通过验证点D是否在此圆上来判断四边形是否有外接圆。(2)由(1)得
三点的圆,通过验证点D是否在此圆上来判断四边形是否有外接圆。(2)由(1)得![]() 的外接圆为
的外接圆为![]() 的方程为
的方程为![]() ,先求得
,先求得![]() ,可得切线
,可得切线![]() 的斜率
的斜率![]() ,切线方程为
,切线方程为![]() ,整理得切线
,整理得切线![]() ,然后求得点
,然后求得点![]() 的坐标,求得
的坐标,求得![]() ,根据基本不等式可得
,根据基本不等式可得![]() ,即为所求。
,即为所求。
试题解析:
(![]() )设过
)设过![]() 三点的外接圆为
三点的外接圆为![]() ,圆心
,圆心![]() ,半径为
,半径为![]() ,
,
则圆![]() 的标准方程为
的标准方程为![]() ,
,
由题意得 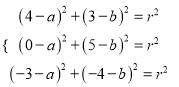 ,解得
,解得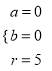
∴ 圆![]() ,
,
验证可得点![]() 在圆
在圆![]() 上。
上。
∴ 四边形![]() 有外接圆,其方程为
有外接圆,其方程为![]() .
.
(![]() )由(1)得
)由(1)得![]() 的外接圆为
的外接圆为![]() 的方程为
的方程为![]() 。
。
由题意得![]() ,
,
∴ 切线![]() 的斜率
的斜率![]() ,从而切线
,从而切线![]() 的方程为
的方程为![]() ,
,
整理得![]() ,
,
又点![]() 在圆
在圆![]() 上,故
上,故![]() ,
,
∴ 切线![]() ,
,
令![]() ,得
,得![]() ,∴
,∴ 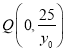 ,
,
令![]() ,得
,得![]() ,∴
,∴ 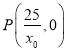 ,
,
∴ ![]() 面积
面积![]() ,
,
∵ ![]() ,
,
∴ ![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
即![]() 面积的最小值为
面积的最小值为![]() ,此时点
,此时点![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知多面体
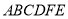 中,四边形
中,四边形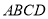 为矩形,
为矩形, 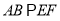 ,
, 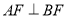 ,平面
,平面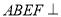 平面
平面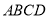 ,
, 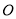 、
、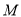 分别为
分别为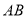 、
、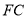 的中点.
的中点.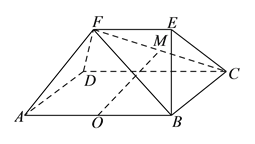
(
 )求证:
)求证: 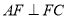 .
.(
 )求证:
)求证: 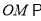 平面
平面 .
.(
 )若过
)若过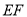 的平面交
的平面交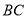 于点
于点 ,交
,交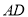 于
于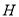 ,求证:
,求证: 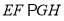 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】矩形
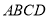 中,
中,  ,
, 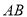 边所在直线的方程为
边所在直线的方程为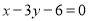 ,点
,点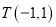 在
在 边所在直线上.
边所在直线上.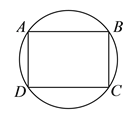
(
 )求
)求 边所在直线的方程.
边所在直线的方程.(
 )求矩形
)求矩形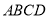 外接圆的方程.
外接圆的方程.(
 )若过点
)若过点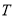 作题(
作题( )中的圆的切线,求切线的方程.
)中的圆的切线,求切线的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 和四边形
和四边形 所在的平面互相垂直.
所在的平面互相垂直.  ,
,  ,
,  .
.
(
 )求证:
)求证:  平面
平面 .
.(
 )求证:
)求证:  平面
平面 .
.(
 )在直线
)在直线 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?并说明理由.
?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, 两个小岛相距
两个小岛相距 海里,
海里, 岛在
岛在 岛的正南方,现在甲船从
岛的正南方,现在甲船从 岛出发,以
岛出发,以 海里/时的速度向
海里/时的速度向 岛行驶,而乙船同时以
岛行驶,而乙船同时以 海里/时的速度离开
海里/时的速度离开 岛向南偏东
岛向南偏东 方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=2
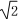 cos
cos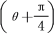 ,直线l的参数方程为
,直线l的参数方程为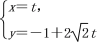 (t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(t为参数),直线l与圆C交于A,B两点,P是圆C上不同于A,B的任意一点.(1)求圆心的极坐标;
(2)求△PAB面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)当
 时,求函数
时,求函数 在
在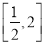 上的最大值和最小值;
上的最大值和最小值;(2)当
 时,是否存在正实数
时,是否存在正实数 ,当
,当 (
( 是自然对数底数)时,函数
是自然对数底数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
相关试题

