【题目】己知函数f(x)=(x﹣l)(log3a)2﹣6(log3a)x+x+l在x∈[0,l]内恒为正值,则a的取值范围是( )
A.﹣1<a< ![]()
B.a< ![]()
C.a> ![]()
D.![]() <a<
<a< ![]()
参考答案:
【答案】D
【解析】解:当a=1时,f(x)=x+1在区间[0,1]上的函数值恒为正实数;
当a≠1时,要使函数f(x)=(x﹣1)(log3a)2﹣6(log3a)x+x+1在区间[0,1]上的函数值恒为正实数,
则有 ![]() ,即
,即 ![]() ,解得
,解得 ![]() .
.
故选:D.
由于一次项系数含有参数,必须分类讨论.当a=1时,显然成立;当a≠1时,要使函数f(x)=(x﹣1)(log3a)2﹣6(log3a)x+x+1在区间[0,1]上的函数值恒为正实数,则有 ![]() ,从而可求a的取值范围.
,从而可求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)当
 时,
时,  恒成立,求
恒成立,求 的取值范围;
的取值范围;(3)求证:当
 时,
时,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若当x∈R时,函数f(x)=a|x|始终满足0<|f(x)|≤1,则函数y=loga|
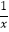 |的图象大致为( )
|的图象大致为( )
A.
B.
C.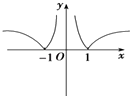
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每年每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).现有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为
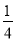 ,
, 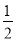 ;两小时以上且不超过三小时还车的概率为
;两小时以上且不超过三小时还车的概率为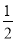 ,
, 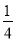 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.(1)求甲、乙都在三到四小时内还车的概率和甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量
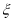 ,求
,求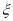 的分布列与数学期望
的分布列与数学期望 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=f(x)的图象是由y=sin2x向右平移
 得到,则下列结论正确的是( )
得到,则下列结论正确的是( )
A.f(0)<f(2)<f(4)
B.f(2)<f(0)<f(4)
C.f(0)<f(4)<f(2)
D.f(4)<f(2)<f(0) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列命题:
①若
 ,则“
,则“ ”是“
”是“ ”成立的充分不必要条件;
”成立的充分不必要条件;②若椭圆
 的两个焦点为
的两个焦点为 ,且弦
,且弦 过点
过点 ,则
,则 的周长为16;
的周长为16;③若命题“
 ”与命题“
”与命题“ 或
或 ”都是真命题,则命题
”都是真命题,则命题 一定是真命题;
一定是真命题;④若命题
 :
:  ,则
,则 :
: 
其中为真命题的是__________(填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)在平面直角坐标系
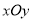 中,曲线
中,曲线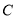 的参数方程是
的参数方程是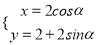 (
(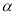 为参数,
为参数, 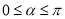 ),以原点
),以原点 为极点,
为极点,  轴的正半轴为极轴,建立极坐标系.
轴的正半轴为极轴,建立极坐标系.(1)写出
 的极坐标方程;
的极坐标方程;(2)若
 为曲线
为曲线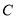 上的两点,且
上的两点,且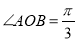 ,求
,求 的范围.
的范围.(Ⅱ)已知函数
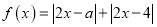 ,
, 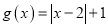 .
.(1)
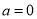 时,解不等式
时,解不等式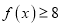 ;
;(2)若对任意
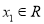 ,存在
,存在 ,使得
,使得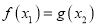 ,求实数
,求实数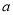 的取值范围.
的取值范围.
相关试题

