Question

【题目】已知函数.

（1）当时，求不等式的解集；

（2）若的解集包含，求的取值范围.

Answer 1

【答案】（1）{x|x≤1，或x≥4}；（2）[－3，0]．

【解析】

试题分析：（1）当时，用分段函数的形式表示出函数的解析式，并分三种情况对其进行讨论，得出相应的不等式的解集，最后可得出该不等式的解集即可；（2）首先将问题的解集包含转化为.当x∈[1，2]时，|x－4|－|x－2|≥|x＋a|，进而转化为－2－a≤x≤2－a，由集合间的包含关系可得出证明.

试题解析：（1）当a＝－3时，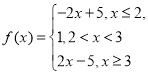

当x≤2时，由f（x）≥3得－2x＋5≥3，解得x≤1；当2<x<3时，f（x）≥3无解；当x≥3时，由f（x）≥3得2x－5≥3，解得x≥4.所以f（x）≥3的解集为{x|x≤1，或x≥4}.

（2）f（x）≤|x－4||x－4|－|x－2|≥|x＋a|.当x∈[1，2]时，|x－4|－|x－2|≥|x＋a|4－x－（2－x）≥|x＋a|－2－a≤x≤2－a.由条件得－2－a≤1且2－a≥2，即－3≤a≤0.故满足条件的a的取值范围是[－3，0].