【题目】设![]() 是各项均不相等的数列,
是各项均不相等的数列, ![]() 为它的前
为它的前![]() 项和,满足
项和,满足![]() .
.
(1)若![]() ,且
,且![]() 成等差数列,求
成等差数列,求![]() 的值;
的值;
(2)若![]() 的各项均不相等,问当且仅当
的各项均不相等,问当且仅当![]() 为何值时,
为何值时, ![]() 成等差数列?试说明理由.
成等差数列?试说明理由.
参考答案:
【答案】(1)![]() (2)当且仅当
(2)当且仅当![]() 时,
时, ![]() 成等差数列
成等差数列
【解析】试题分析:(1)根据![]() 解出
解出![]() (用
(用![]() 表示),再根据
表示),再根据![]() 成等差数列,得
成等差数列,得![]() ,代入解出
,代入解出![]() 的值;(2)先研究
的值;(2)先研究![]() 成等差数列时
成等差数列时![]() 为何值,同(1)根据
为何值,同(1)根据![]() 解出
解出![]() ,
, ![]() (用
(用![]() 表示),再根据
表示),再根据![]() 成等差数列解出
成等差数列解出![]() 的值
的值![]() ;再证明
;再证明![]() 时,
时, ![]() 成等差数列,实际上求出
成等差数列,实际上求出![]() 这个关系式.
这个关系式.
试题解析:解:(1)令![]() ,得
,得![]() ,
,
又由![]() 成等差数列,所以
成等差数列,所以![]() ,
,
解得![]() .
.
(2)当且仅当![]() 时,
时, ![]() 成等差数列,
成等差数列,
证明如下:
由已知![]() ,当
,当![]() 时,
时, ![]() ,
,
两式相减得![]() ,即
,即![]() ,
,
由于![]() 个各项均不相等,所以
个各项均不相等,所以![]() ,
,
当![]() 时,所以
时,所以![]()
两式相减可得![]() ,
,
①当![]() ,得
,得![]() ,当
,当![]() 时,所以
时,所以![]() ,
,
![]() ,所以
,所以![]() ,
,
故![]() 成等差数列.
成等差数列.
②再证当![]() 成等差数列时,
成等差数列时, ![]() ,
,
因为![]() 成等差数列,
成等差数列,
所以![]() ,可得
,可得![]() ,
,
所以![]() ,
,
所以当且仅当![]() 时,
时, ![]() 成等差数列.
成等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,
中,  .
.(1)若
 是
是 的中点,求证:
的中点,求证:  平面
平面 ;
;(2)若
 ,求证:平面
,求证:平面 平面
平面 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
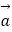 =(cosx,cosx),
=(cosx,cosx), 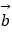 =(sinx,﹣cosx),记函数f(x)=2
=(sinx,﹣cosx),记函数f(x)=2 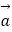
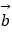 +1,其中x∈R.
+1,其中x∈R.
(Ⅰ)求函数f(x)的最小正周期及函数f(x)的图象的对称中心的坐标;
(Ⅱ)若α∈(0, ),且f(
),且f(  )=
)=  ,求cos2α的值.
,求cos2α的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
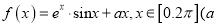 为常数).
为常数).(1)当
 时,求
时,求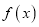 的单调区间;
的单调区间;(2)若
 在区间
在区间 的极大值、极小值各有一个,求实数
的极大值、极小值各有一个,求实数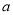 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2+(a2﹣1)x+a﹣2=0的两根满足(x1﹣1)(x2﹣1)<0,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足|
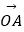 |=|
|=| 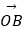 |=
|= 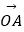
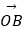 =2,则点集{P|
=2,则点集{P| 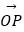 =x
=x 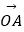 +y
+y 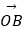 ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】先将函数y=f(x)的图象向左平移
 个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若函数y=g(x)与y=f(x)的图象关于点M( ,2)对称,求函数y=g(x)在[0,
,2)对称,求函数y=g(x)在[0,  ]上的最小值和最大值.
]上的最小值和最大值.
相关试题

