【题目】先将函数y=f(x)的图象向左平移 ![]() 个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
个单位,然后再将所得图象上所有点的纵坐标不变,横坐标伸长到原来的2倍,最后再将所得图象向上平移1个单位,得到函数y=sinx的图象.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)若函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,求函数y=g(x)在[0,
,2)对称,求函数y=g(x)在[0, ![]() ]上的最小值和最大值.
]上的最小值和最大值.
参考答案:
【答案】解:(Ⅰ)由题意可得,把函数y=sinx的图象向下平移1个单位得y=sinx﹣1的图象,
然后再将y=sinx﹣1图象上所有点的纵坐标不变,横坐标缩短到原来的 ![]() 倍,得到y=sin2x﹣1的图象,
倍,得到y=sin2x﹣1的图象,
最后将函数y=sin2x﹣1的图象向右平移 ![]() 个单位得y=sin2(x﹣
个单位得y=sin2(x﹣ ![]() )﹣1的图象,
)﹣1的图象,
所以函数y=f(x)的表达式是y=sin(2x﹣ ![]() )﹣1.
)﹣1.
(Ⅱ)设函数y=f(x)=sin(2x﹣ ![]() )﹣1图象任意一点为P(m,n),点P(m,n)关于点M(
)﹣1图象任意一点为P(m,n),点P(m,n)关于点M( ![]() ,2)对称点为Q(x,y),
,2)对称点为Q(x,y),
由于函数y=g(x)与y=f(x)的图象关于点M( ![]() ,2)对称,点Q(x,y)是函数y=g(x)图象上的点.
,2)对称,点Q(x,y)是函数y=g(x)图象上的点.
由中点坐标公式可得m+x= ![]() 且 n+y=4,即 m=
且 n+y=4,即 m= ![]() ﹣x且 n=4﹣y.
﹣x且 n=4﹣y.
由点P(m,n)在函数 y=sin(2x﹣ ![]() )﹣1的图象上,可得n=sin(2m﹣
)﹣1的图象上,可得n=sin(2m﹣ ![]() )﹣1,即有4﹣y=sin[2(
)﹣1,即有4﹣y=sin[2( ![]() ﹣x)﹣
﹣x)﹣ ![]() )]﹣1,
)]﹣1,
化简得y=sin(2x﹣ ![]() )+5,所以函数y=g(x)的解析式为y=sin(2x﹣
)+5,所以函数y=g(x)的解析式为y=sin(2x﹣ ![]() )+5.
)+5.
由于x∈[0, ![]() ],所以y=g(x)=sin(2x﹣
],所以y=g(x)=sin(2x﹣ ![]() )+5,根据2x﹣
)+5,根据2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],y=sin(2x﹣
],y=sin(2x﹣ ![]() )+5∈[4,5+
)+5∈[4,5+ ![]() ],
],
函数y=g(x)在[0, ![]() ]的最小值和最大值分别为4和5+
]的最小值和最大值分别为4和5+ ![]()
【解析】(Ⅰ)由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.(Ⅱ)由条件利用两个函数的图象关于某个点对称的性质,正弦函数的定义域和值域,求得函数y=g(x)在[0, ![]() ]的最小值和最大值.
]的最小值和最大值.
【考点精析】解答此题的关键在于理解函数y=Asin(ωx+φ)的图象变换的相关知识,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
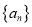 是各项均不相等的数列,
是各项均不相等的数列,  为它的前
为它的前 项和,满足
项和,满足 .
.(1)若
 ,且
,且 成等差数列,求
成等差数列,求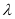 的值;
的值;(2)若
 的各项均不相等,问当且仅当
的各项均不相等,问当且仅当 为何值时,
为何值时,  成等差数列?试说明理由.
成等差数列?试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2+(a2﹣1)x+a﹣2=0的两根满足(x1﹣1)(x2﹣1)<0,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足|
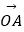 |=|
|=| 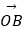 |=
|= 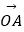
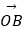 =2,则点集{P|
=2,则点集{P| 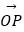 =x
=x 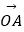 +y
+y 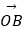 ,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民用水拟实行阶梯水价,每人月用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费,从该市随机调查了10000位居民,获得了他们某月的用水量数据,整理得到如图频率分布直方图:

(1)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(2)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高一 、高二 、高三三个年级共有
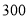 名教师,为调查他们的备课时间情况,通过分层
名教师,为调查他们的备课时间情况,通过分层抽样获得了
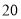 名教师一周的备课时间 ,数据如下表(单位 :小时):
名教师一周的备课时间 ,数据如下表(单位 :小时):高一年级
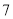
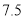

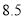
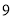
高二年级
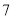
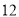

高三年级
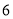
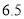

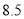
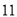
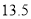
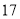
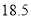
(1)试估计该校高三年级的教师人数 ;
(2)从高一年级和高二年级抽出的教师中,各随机选取一人,高一年级选出的人记为甲 ,高二年级选出的人记为乙 ,求该周甲的备课时间不比乙的备课时间长的概率 ;
(3)再从高一、高二、高三三个年级中各随机抽取一名教师,他们该周的备课时间分别是
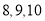 (单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为
(单位: 小时),这三个数据与表格中的数据构成的新样本的平均数记为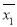 ,表格中的数据平均数记为
,表格中的数据平均数记为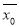 ,试判断
,试判断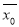 与
与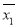 的大小. (结论不要求证明)
的大小. (结论不要求证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.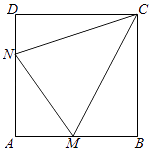
相关试题

