搜索
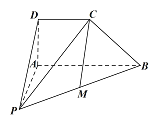
【题目】如图，在四棱锥
中, 
.
（1）若
是
的中点，求证： 
平面
；
（2）若
，求证：平面
平面
.
参考答案：
【答案】（1）见解析（2）见解析
【解析】试题分析：（1）取
的中点
，利用平几知识证明四边形
是平行四边形，即得
.最后根据线面垂直判定定理得
平面
；（2）由平均知识计算
，再由
，根据线面垂直判定定理得
面
,最后根据面面垂直判定定理得平面
平面
.
试题解析：解（1）取
的中点
，连接
和
，由因为
是
的中点，
所以
是
的中位线，所以
，
由题意
，所以
，
所以四边形
是平行四边形，所以
.因为
，所以
平面
；
(2)由题意，在直角梯形
中，经计算可证得
，又
面
，
, 
面
,又
面
，所以平面
平面
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有下列四个说法：
①若函数f（x）=asinx+cosx（x∈R）的图象关于直线x=
对称，则a=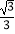 
；
②已知向量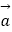
=（1，2）， 
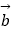=（﹣2，m），若 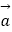与 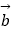的夹角为钝角，则m＜1；
③当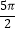
＜α＜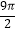 
时，函数f（x）=sinx﹣logax有三个零点；
④函数f（x）=xsinx在[﹣
，0]上单调递减，在[0， ]上单调递增．
其中正确的是（填上所有正确说法的序号） -
科目： 来源： 题型：
查看答案和解析>>【题目】函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）（x∈R）的部分图象如图所示．
（Ⅰ）求函数f（x）的解析式并求函数f（x）的单调递增区间；
（Ⅱ）求函数f（x）的最小值并指出函数f（x）取最小值时相应的x的值．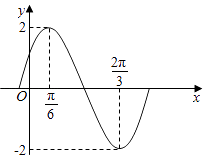
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=sin2
+ 
sinωx﹣ （ω＞0），x∈R，若f（x）在区间（π，2π）内没有零点，则ω的取值范围是（ ）
A.（0，
]
B.（0，
]∪[ 
，1）
C.（0， ]
D.（0， ]∪[ ， ] -
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量
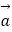=（cosx，cosx）， 
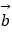=（sinx，﹣cosx），记函数f（x）=2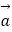 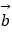+1，其中x∈R．
（Ⅰ）求函数f（x）的最小正周期及函数f（x）的图象的对称中心的坐标；
（Ⅱ）若α∈（0，
），且f（ 
）= 
，求cos2α的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设
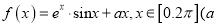为常数）.（1）当
时，求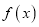
的单调区间；（2）若
在区间
的极大值、极小值各有一个，求实数
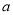的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】设
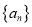是各项均不相等的数列， 
为它的前
项和，满足
.（1）若
，且
成等差数列，求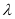
的值；（2）若
的各项均不相等，问当且仅当
为何值时， 
成等差数列？试说明理由.
相关试题
