搜索
【题目】关于x的方程x2+（a2﹣1）x+a﹣2=0的两根满足（x1﹣1）（x2﹣1）＜0，则a的取值范围是 ．
参考答案：
【答案】﹣2＜a＜1
【解析】解：∵关于x的方程x2+（a2﹣1）x+a﹣2=0的两根分别为x1、x2 ， ∴x1+x2=1﹣a2 ， x1x2=a﹣2；
又（x1﹣1）（x2﹣1）＜0，
∴x1x2﹣（x1+x2）+1＜0，
∴（a﹣2）﹣（1﹣a2）+1＜0，
即a2+a﹣2＜0；
解得﹣2＜a＜1，
∴a的取值范围是﹣2＜a＜1．
【考点精析】通过灵活运用解一元二次不等式，掌握求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量
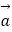=（cosx，cosx）， 
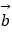=（sinx，﹣cosx），记函数f（x）=2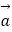 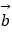+1，其中x∈R．
（Ⅰ）求函数f（x）的最小正周期及函数f（x）的图象的对称中心的坐标；
（Ⅱ）若α∈（0，
），且f（ 
）= 
，求cos2α的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】设
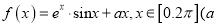为常数）.（1）当
时，求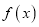
的单调区间；（2）若
在区间
的极大值、极小值各有一个，求实数
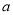的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】设
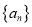是各项均不相等的数列， 
为它的前
项和，满足
.（1）若
，且
成等差数列，求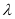
的值；（2）若
的各项均不相等，问当且仅当
为何值时， 
成等差数列？试说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，O是坐标原点，两定点A，B满足|
|=| 
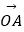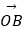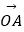
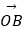|= =2，则点集{P| 
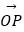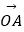=x +y 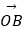，|x|+|y|≤1，x，y∈R}所表示的区域的面积是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】先将函数y=f（x）的图象向左平移
个单位，然后再将所得图象上所有点的纵坐标不变，横坐标伸长到原来的2倍，最后再将所得图象向上平移1个单位，得到函数y=sinx的图象．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）若函数y=g（x）与y=f（x）的图象关于点M（
，2）对称，求函数y=g（x）在[0， 
]上的最小值和最大值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某市居民用水拟实行阶梯水价，每人月用水量中不超过w立方米的部分按4元/立方米收费，超出w立方米的部分按10元/立方米收费，从该市随机调查了10000位居民，获得了他们某月的用水量数据，整理得到如图频率分布直方图：
（1）如果w为整数，那么根据此次调查，为使80%以上居民在该月的用水价格为4元/立方米，w至少定为多少？
（2）假设同组中的每个数据用该组区间的右端点值代替，当w=3时，估计该市居民该月的人均水费．
相关试题
