【题目】某化工厂生产甲、乙两种肥料,生产1车皮甲种肥料能获得利润10000元,需要的主要原料是磷酸盐4吨,硝酸盐8吨;生产1车皮乙种肥料能获得利润5000元,需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存有磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种肥料.问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?
参考答案:
【答案】生产甲种、乙种肥料各2车皮,能够产生最大利润,最大利润为3万元.
【解析】
设生产甲种肥料x车皮、乙种肥料y车皮能够产生利润z万元,列出线性约束条件,再利用线性规划求解.
设生产甲种肥料x车皮、乙种肥料y车皮能够产生利润z万元.
目标函数为z=x+0.5y,
约束条件为: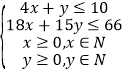 ,
,
可行域如图中阴影部分的整点.
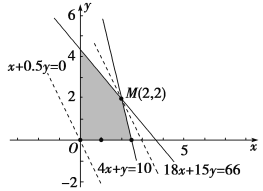
当直线y=-2x+2z经过可行域上的点M时,截距2z最大,即z最大.
解方程组![]() 得:M点坐标为(2,2).
得:M点坐标为(2,2).
所以zmax=x+0.5y=3.
所以生产甲种、乙种肥料各2车皮,能够产生最大利润,最大利润为3万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年入冬以来,各地雾霾天气频发,
 频频爆表(
频频爆表( 是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与
是指直径小于或等于2.5微米的颗粒物),各地对机动车更是出台了各类限行措施,为分析研究车流量与 的浓度是否相关,某市现采集周一到周五某一时间段车流量与
的浓度是否相关,某市现采集周一到周五某一时间段车流量与 的数据如下表:
的数据如下表:时间
周一
周二
周三
周四
周五
车流量
 (万辆)
(万辆)50
51
54
57
58
 的浓度
的浓度 (微克/立方米)
(微克/立方米)69
70
74
78
79
(1)请根据上述数据,在下面给出的坐标系中画出散点图;

(2)试判断
 与
与 是否具有线性关系,若有请求出
是否具有线性关系,若有请求出 关于
关于 的线性回归方程
的线性回归方程 ,若没有,请说明理由;
,若没有,请说明理由;(3)若周六同一时间段的车流量为60万辆,试根据(2)得出的结论,预报该时间段的
 的浓度(保留整数).
的浓度(保留整数).参考公式:

 ,
, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=f(x)的图象是以原点为圆心、1为半径的两段圆弧,如图所示.则不等式f(x)>f(-x)+x的解集为( )

A.
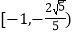 ∪(0,1]
∪(0,1]B. [-1,0)∪
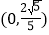
C.
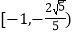 ∪
∪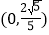
D.
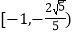 ∪
∪
-
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长为1的正方体ABCD﹣A'B'C'D'中,E是AA'的中点,P是三角形BDC'内的动点,EP⊥BC',则P的轨迹长为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】整改校园内一块长为15 m,宽为11 m的长方形草地(如图A),将长减少1 m,宽增加1 m(如图B).问草地面积是增加了还是减少了?假设长减少x m,宽增加x m(x>0),试研究以下问题:

x取什么值时,草地面积减少?
x取什么值时,草地面积增加?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (m>0)的最大值为2.
(m>0)的最大值为2.
(1)求函数,f(x)在[0,π]上的单调递减区间;
(2)△ABC中,a,b,c分别是角A,B,C所对的边,C=60°,c=3,且 ,求△ABC的面积.
,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)=ax2+bx+c(a,b,c∈R)满足:对任意实数x,都有f(x)≥x,且当x∈(1,3)时,有f(x)≤
 (x+2)2成立.
(x+2)2成立.(1)证明:f(2)=2;
(2)若f(-2)=0,求f(x)的表达式;
(3)设g(x)=f(x)-
 x,x∈[0,+∞),若g(x)图象上的点都位于直线y=
x,x∈[0,+∞),若g(x)图象上的点都位于直线y= 的上方,求实数m的取值范围.
的上方,求实数m的取值范围.
相关试题

