【题目】已知四棱锥![]() 中,底面
中,底面![]() 为平行四边形,点
为平行四边形,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上.
上.

(1)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 满足
满足![]() ,则
,则![]() 点满足什么条件时,
点满足什么条件时,![]() 面
面![]() .
.
参考答案:
【答案】(1)证明见解析;(2)当点![]() 是
是![]() 的中点时,
的中点时,![]() 面
面![]() .
.
【解析】
(1)由![]() 可证明出
可证明出![]() ,再由
,再由![]() ,可得出
,可得出![]() ,利用直线与平面平行的判定定理可证明出
,利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ,同理证明
,同理证明![]() 平面
平面![]() ,再由平面与平面平行的判定定理可证明出平面
,再由平面与平面平行的判定定理可证明出平面![]() 平面
平面![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,利用直线与平面平行的判定定理证明出
,利用直线与平面平行的判定定理证明出![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,再利用平面与平面平行的判定定理证明出平面
,再利用平面与平面平行的判定定理证明出平面![]() 平面
平面![]() ,于此可得出
,于此可得出![]() 平面
平面![]() .
.
(1)![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,则点
,则点![]() 为
为![]() 的中点,下面证明:当点
的中点,下面证明:当点![]() 为
为![]() 的中点时,
的中点时,![]() 平面
平面![]() .
.

![]() 且
且![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 的中点,
的中点,
又![]() 点
点![]() 为
为![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,同理,
,同理,![]() 平面
平面![]() .
.
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
因此,当点![]() 是
是![]() 的中点时,
的中点时,![]() 面
面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 .
.(1)若函数
 在
在 处取得极值,求实数
处取得极值,求实数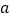 的值;
的值;(2)在(1)的结论下,若关于
 的不等式
的不等式 ,当
,当 时恒成立,求
时恒成立,求 的值;
的值;(3)令
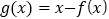 ,若关于
,若关于 的方程
的方程 在
在 内至少有两个解,求出实数
内至少有两个解,求出实数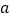 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数)。在以坐标原点为极点,
为参数)。在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 。
。(1)写出曲线
 ,
, 的普通方程;
的普通方程;(2)过曲线
 的左焦点且倾斜角为
的左焦点且倾斜角为 的直线
的直线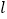 交曲线
交曲线 于
于 两点,求
两点,求 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年
 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在 岁之间的
岁之间的 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为 .
.关注
不关注
合计
年轻人

中老年人
合计



(1)根据已知条件完成上面的
 列联表,并判断能否有
列联表,并判断能否有 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?(2)现已用分层抽样的办法从中老年人中选取了
 人进行问卷调查.若再从这
人进行问卷调查.若再从这 人中选取
人中选取 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的 人中恰有
人中恰有 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.附:参考公式
 ,其中
,其中 .
.临界值表:






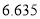

-
科目: 来源: 题型:
查看答案和解析>>【题目】过点
 作抛物线
作抛物线 的两条切线,切点分别为
的两条切线,切点分别为 ,
, ,
, ,
, 分别交
分别交 轴于
轴于 ,
, 两点,
两点, 为坐标原点,则
为坐标原点,则 与
与 的面积之比为( )
的面积之比为( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四面体
 中,
中, ,则四面体体积最大时,它的外接球半径
,则四面体体积最大时,它的外接球半径 _________.
_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 在
在 上有定义,要使函数
上有定义,要使函数 有定义,则a的取值范围为
有定义,则a的取值范围为A.
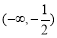 ;B.
;B. C.
C. ;D.
;D.
相关试题

