【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(2)在(1)的结论下,若关于![]() 的不等式
的不等式![]() ,当
,当![]() 时恒成立,求
时恒成立,求![]() 的值;
的值;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 在
在![]() 内至少有两个解,求出实数
内至少有两个解,求出实数![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() ;(3) 实数
;(3) 实数![]() 的范围是
的范围是![]() .
.
【解析】分析:(1)根据![]() 求得
求得![]() ;(2)由题意结合分离参数可得
;(2)由题意结合分离参数可得![]() 对
对![]() 恒成立,构造函数
恒成立,构造函数![]() ,
,![]() ,利用导数可得
,利用导数可得![]() ,故得
,故得![]() ,又
,又![]() ,所以得到
,所以得到![]() .
.
(3)由题意![]() ,令
,令![]() ,构造函数
,构造函数![]() ,则由题意得可得方程
,则由题意得可得方程![]() 在区间
在区间![]() 上只少有两个解.然后分类讨论可得实数
上只少有两个解.然后分类讨论可得实数![]() 的范围是
的范围是![]() .
.
详解:(1)∵![]() ,
,
∴![]() ,
,
又函数![]() 在
在![]() 处取得极值,
处取得极值,
∴![]() ,解得
,解得![]() .
.
经验证知![]() 满足条件,
满足条件,
∴![]() .
.
(2)当![]() 时,
时,![]() ,
,
∴![]() .
.
由题意得![]() 对
对![]() 恒成立,
恒成立,
∴![]() 对
对![]() 恒成立.
恒成立.
令![]() ,
,![]() ,
,
则![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
(3)由题意得![]() ,
,
令![]() ,设
,设![]()
则方程![]() 在区间
在区间![]() 上只少有两个解,
上只少有两个解,
又![]() ,
,
∴方程![]() 在区间
在区间![]() 上有解,
上有解,
由于![]() ,
,
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() ,
,
∴方程在区间![]() 上无解;
上无解;
②当![]() 时,
时,![]() ,同①可得方程无解;
,同①可得方程无解;
③当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,且
上递减,且![]() ,
,
要使方程![]() 在区间
在区间![]() 上有解,则
上有解,则![]() ,即
,即![]() ,
,
∴![]() ;
;
④当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,且
上递减,且![]() ,
,
此时方程![]() 在
在![]() 内必有解;
内必有解;
⑤当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,且
上递减,且![]() ,
,
∴方程![]() 在区间
在区间![]() 内无解.
内无解.
综上可得实数![]() 的范围是
的范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
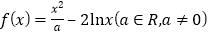 .
.(1)讨论函数
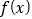 的单调性;
的单调性;(2) 若函数
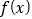 有两个零点
有两个零点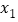 ,
, 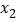
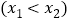 ,且
,且 ,证明:
,证明: 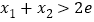 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面
的底面 为直角梯形,
为直角梯形, ,
, ,
, ,
, 为正三角形.
为正三角形.
(1)若点
 是棱
是棱 的中点,求证:
的中点,求证: 平面
平面 ;
;(2)若平面
 ⊥平面
⊥平面 ,在(1)的条件下,试求四棱锥
,在(1)的条件下,试求四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,直线
中,直线 的参数方程为
的参数方程为 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 ,且直线
,且直线 经过曲线
经过曲线 的左焦点
的左焦点 .
.(1)求
 的值及直线
的值及直线 的普通方程;
的普通方程;(2)设曲线
 的内接矩形的周长为
的内接矩形的周长为 ,求
,求 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数)。在以坐标原点为极点,
为参数)。在以坐标原点为极点, 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 。
。(1)写出曲线
 ,
, 的普通方程;
的普通方程;(2)过曲线
 的左焦点且倾斜角为
的左焦点且倾斜角为 的直线
的直线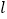 交曲线
交曲线 于
于 两点,求
两点,求 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】2019年
 月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在
月湖北潜江将举办第六届“中国湖北(潜江)龙虾节”,为了解不同年龄的人对“中国湖北(潜江)龙虾节”关注程度,某机构随机抽取了年龄在 岁之间的
岁之间的 人进行调查,经统计“年轻人”与“中老年人”的人数之比为
人进行调查,经统计“年轻人”与“中老年人”的人数之比为 .
.关注
不关注
合计
年轻人

中老年人
合计



(1)根据已知条件完成上面的
 列联表,并判断能否有
列联表,并判断能否有 的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?
的把握认为关注“中国湖北(潜江)龙虾节”是否和年龄段有关?(2)现已用分层抽样的办法从中老年人中选取了
 人进行问卷调查.若再从这
人进行问卷调查.若再从这 人中选取
人中选取 人进行面对面询问,求事件“选取的
人进行面对面询问,求事件“选取的 人中恰有
人中恰有 人关注“中国湖北(潜江)龙虾节””的概率.
人关注“中国湖北(潜江)龙虾节””的概率.附:参考公式
 ,其中
,其中 .
.临界值表:






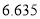

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 中,底面
中,底面 为平行四边形,点
为平行四边形,点 、
、 、
、 分别在
分别在 、
、 、
、 上.
上.
(1)若
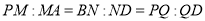 ,求证:平面
,求证:平面 平面
平面 ;
;(2)若
 满足
满足 ,则
,则 点满足什么条件时,
点满足什么条件时, 面
面 .
.
相关试题

