【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的最小值;
的最小值;
(Ⅱ)设![]() (
(![]() ),讨论函数
),讨论函数![]() 的单调性;
的单调性;
(Ⅲ)若斜率为![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时,![]() 在区间
在区间![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() 在
在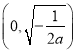 内单调递增,在
内单调递增,在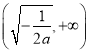 内单调递减.(Ⅲ)见解析.
内单调递减.(Ⅲ)见解析.
【解析】
试题分析:(Ⅰ)求函数![]() 的导数
的导数![]() ,由
,由![]() 与
与![]() 求函数的单调区间与单调性,从而可得
求函数的单调区间与单调性,从而可得![]() ;(Ⅱ)由已知可知
;(Ⅱ)由已知可知![]() ,
,![]() ,分
,分![]() 与
与![]() 分别讨论导数的符号可得函数
分别讨论导数的符号可得函数![]() 的单调区间;(Ⅲ)
的单调区间;(Ⅲ)![]() ,则不等式
,则不等式![]()
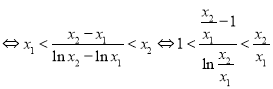 ,令
,令![]() ,只要证不等式
,只要证不等式![]() (
(![]() )即可,分别构造函数
)即可,分别构造函数![]() (
(![]() )与
)与![]() (
(![]() ),可证
),可证![]() 成立.
成立.
试题解析: (Ⅰ)![]() (
(![]() ),……(1分)
),……(1分)
令![]() ,得
,得![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
则![]() 在
在![]() 内递减,在
内递减,在![]() 内递增,…………(2分)
内递增,…………(2分)
所以当![]() 时,函数
时,函数![]() 取得最小值,且
取得最小值,且![]() ……(3分)
……(3分)
(Ⅱ)![]() ,
,![]() (
(![]() ),…………(4分)
),…………(4分)
当![]() 时,恒有
时,恒有![]() ,
,![]() 在区间
在区间![]() 内是增函数;……(5分)
内是增函数;……(5分)
当![]() 时,令
时,令![]() ,即
,即![]() ,解得
,解得![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,………(6分)
,………(6分)
综上,当![]() 时,
时,![]() 在区间
在区间![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() 在
在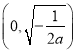 内单调递增,在
内单调递增,在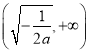 内单调递减.………(7分)
内单调递减.………(7分)
(Ⅲ)证明:![]() ,要证明
,要证明![]() ,
,
即证![]() ,………(8分)
,………(8分)
等价于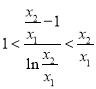 ,令
,令![]() (由
(由![]() ,知
,知![]() ),
),
则只需证![]() ,由
,由![]() ,知
,知![]() ,故等价于
,故等价于![]() (
(![]() )(
)(![]() )……(9分)
)……(9分)
①设![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,当
内是增函数,当![]() 时,
时,![]() ,所以
,所以![]() ;…………(10分)
;…………(10分)
②设![]() (
(![]() ),则
),则![]() (
(![]() ),所以
),所以![]() 在
在![]() 内是增函数,所以当
内是增函数,所以当![]() 时,
时,![]() ,即
,即![]() (
(![]() ).……(11分)
).……(11分)
由①②知(![]() )成立,所以
)成立,所以![]() .……(12分)
.……(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
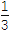 x3+
x3+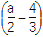 x2+
x2+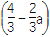 x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围. -
科目: 来源: 题型:
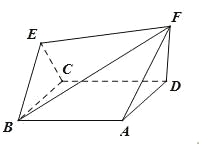
查看答案和解析>>【题目】如图,棱形
 与正三角形
与正三角形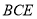 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直, 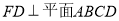 ,且
,且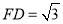 .
.
(1)求证:
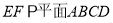 ;
;(2)若
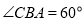 ,求二面角
,求二面角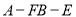 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】画出下列函数的图像,并根据图像说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数。
(1)y=x2-5x-6; (2)y=|4-x2|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
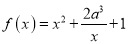 .
.(1)若曲线
 在点
在点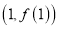 处的切线与直线
处的切线与直线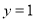 平行,求
平行,求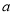 的值;
的值;(2)若
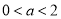 ,求函数
,求函数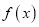 在区间
在区间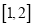 上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
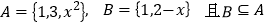
⑴求实数
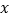 的值;
的值;⑵若
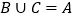 ,求集合
,求集合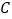 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=elnx,g(x)=
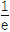 f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)(1)求函数g(x)的极大值;
(2)求证:1+
 +
+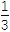 +…+
+…+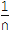 >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*).
相关试题

