【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
参考答案:
【答案】(1)1(2)见解析
【解析】试题分析:(1)本问主要考查导数几何意义,由于曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,根据两直线平行斜率相等得
平行,根据两直线平行斜率相等得![]() ,对函数
,对函数![]() 求导,带入
求导,带入![]() ,即可求出
,即可求出![]() 的值;(2)本问考查利用导数研究函数最值,
的值;(2)本问考查利用导数研究函数最值, ![]() ,显然
,显然![]() 时,
时, ![]() ,然后对
,然后对![]() 进行讨论,分别讨论
进行讨论,分别讨论![]() ,
, ![]() 时
时![]() 在区间
在区间![]() 上的单调性,进而可以求出最小值.这里重点考查分类讨论思想方法在解题中的应用.
上的单调性,进而可以求出最小值.这里重点考查分类讨论思想方法在解题中的应用.
试题解析: ![]() .
.
(1)由题意可得![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
在点![]() 处的切线为
处的切线为![]() ,与直线
,与直线![]() 平行.
平行.
故所求的![]() 值为
值为![]() .
.
(2)![]() ,可得
,可得![]() .
.
①![]() 时,
时, ![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上递增,
上递增,
所以![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
②当![]() 时,
时, ![]() ,
, ![]() 随
随![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
| - |
| + |
| ↓ | 极小 | ↑ |
由上表可知![]() 在
在![]() 的最小值为
的最小值为![]() .
.
综上可知:
当![]() 时,
时, ![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,
时, ![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱形
 与正三角形
与正三角形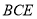 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直, 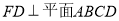 ,且
,且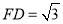 .
.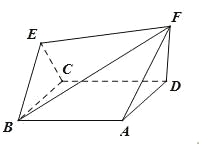
(1)求证:
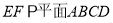 ;
;(2)若
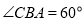 ,求二面角
,求二面角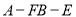 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】画出下列函数的图像,并根据图像说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数。
(1)y=x2-5x-6; (2)y=|4-x2|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
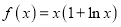 .
.(Ⅰ)求函数
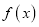 的最小值;
的最小值;(Ⅱ)设
 (
(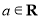 ),讨论函数
),讨论函数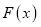 的单调性;
的单调性;(Ⅲ)若斜率为
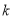 的直线与曲线
的直线与曲线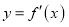 交于
交于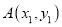 ,
,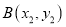 两点,其中
两点,其中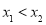 ,求证:
,求证: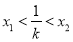 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
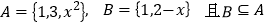
⑴求实数
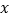 的值;
的值;⑵若
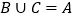 ,求集合
,求集合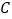 。
。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=elnx,g(x)=
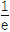 f(x)-(x+1).(e=2.718……)
f(x)-(x+1).(e=2.718……)(1)求函数g(x)的极大值;
(2)求证:1+
 +
+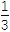 +…+
+…+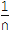 >ln(n+1)(n∈N*).
>ln(n+1)(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:
 为
为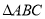 所在平面外一点,
所在平面外一点, 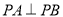 ,
, 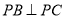 ,
, 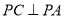 ,
, 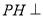 平面
平面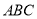 于
于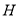 .求证:
.求证: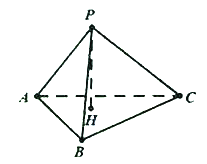
(1)
 是
是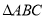 的垂心;
的垂心;(2)
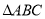 为锐角三角形.
为锐角三角形.
相关试题

