【题目】已知函数f(x)=![]() x3+
x3+![]() x2+
x2+![]() x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
参考答案:
【答案】见解析
【解析】
解 因为f′(x)=x2+![]() x+
x+![]() =
=![]() (x+a-2),所以令f′(x)=0,
(x+a-2),所以令f′(x)=0,
解得x1=![]() ,x2=2-a.
,x2=2-a.
由0<a<1,知1<2-a<2.
所以令f′(x)>0,得x<![]() ,或x>2-a;
,或x>2-a;
令f′(x)<0,得![]() <x<2-a,
<x<2-a,
所以函数f(x)在(1,2-a)上单调递减,在(2-a,2)上单调递增.
所以函数f(x)在[1,2]上的最小值为f(2-a)=![]() (2-a)2,最大值为max{f(1),f(2)}=max
(2-a)2,最大值为max{f(1),f(2)}=max![]() .
.
因为当0<a≤![]() 时,
时,![]() -
-![]() ≥
≥![]() a;
a;
当![]() <a<1时,
<a<1时,![]() a>
a>![]() -
-![]() ,
,
由对任意x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,得2f(x)min>f(x)max(x∈[1,2]).
所以当0<a≤![]() 时,必有2×
时,必有2×![]() (2-a)2>
(2-a)2>![]() -
-![]() ,
,
结合0<a≤![]() 可解得1-
可解得1-![]() <a≤
<a≤![]() ;
;
当![]() <a<1时,必有2×
<a<1时,必有2×![]() (2-a)2>
(2-a)2>![]() a,
a,
结合![]() <a<1可解得
<a<1可解得![]() <a<2-
<a<2-![]() .
.
综上,知所求实数a的取值范围是1-![]() <a<2-
<a<2-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数
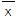 ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数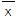 ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数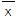 ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.A.①② B.③④
C.③④⑤ D.④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式;
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围;
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式
 -kx+1≤0的解集非空,则k的取值范围为________.
-kx+1≤0的解集非空,则k的取值范围为________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,棱形
 与正三角形
与正三角形 的边长均为2,它们所在平面互相垂直,
的边长均为2,它们所在平面互相垂直, 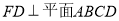 ,且
,且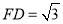 .
.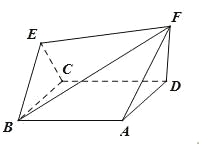
(1)求证:
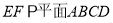 ;
;(2)若
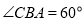 ,求二面角
,求二面角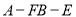 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】画出下列函数的图像,并根据图像说出函数y=f(x)的单调区间,以及在各单调区间上函数y=f(x)是增函数还是减函数。
(1)y=x2-5x-6; (2)y=|4-x2|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
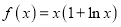 .
.(Ⅰ)求函数
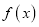 的最小值;
的最小值;(Ⅱ)设
 (
(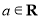 ),讨论函数
),讨论函数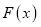 的单调性;
的单调性;(Ⅲ)若斜率为
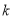 的直线与曲线
的直线与曲线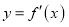 交于
交于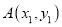 ,
,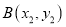 两点,其中
两点,其中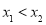 ,求证:
,求证: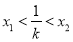 .
.
相关试题

