【题目】已知函数![]() .
.
(1)当![]() 时,函数
时,函数![]() 恰有两个不同的零点,求实数
恰有两个不同的零点,求实数![]() 的值;
的值;
(2)当![]() 时,
时,
① 若对于任意![]() ,恒有
,恒有![]() ,求
,求![]() 的取值范围;
的取值范围;
② 若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() .
.
参考答案:
【答案】(1) ![]() ;(2)①.
;(2)①. ![]() ;②.
;②. 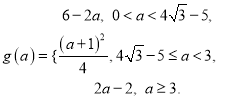
【解析】试题分析:(1)当![]() 时,考虑
时,考虑![]() 的解,化简后得到
的解,化简后得到![]() 或者
或者![]() ,它们共有两个不同的零点,所以
,它们共有两个不同的零点,所以![]() 必有解
必有解![]() ,从而
,从而![]() .
.
(2)![]() 在
在![]() 上恒成立等价于
上恒成立等价于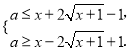 在
在![]() 上恒成立,因此考虑
上恒成立,因此考虑![]() 在
在![]() 上的最小值和
上的最小值和![]() 在
在![]() 上的最大值即可得到
上的最大值即可得到![]() 的取值范围.
的取值范围.
(3)![]() 可化为
可化为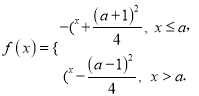 ,则当
,则当![]() 或
或![]() 时,
时, ![]() 在
在![]() 上递增;当
上递增;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,两类情形都可以求得函数的最大值.当
上单调递减,两类情形都可以求得函数的最大值.当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,因此
上单调递增,因此![]() ,比较
,比较![]() 的大小即可得到
的大小即可得到![]() 的表达式.
的表达式.
解析:(1)当![]() 时,
时, ![]() ,由
,由![]() 解得
解得![]() 或
或![]() ,由
,由![]() 解得
解得![]() 或
或![]() .因为
.因为![]() 恰有两个不同的零点且
恰有两个不同的零点且![]() ,所以
,所以![]() ,或
,或 ![]() ,所以
,所以![]() .
.
(2)当![]() 时,
时, ![]() ,
,
①因为对于任意![]() ,恒有
,恒有![]() , 即
, 即 ![]() ,即
,即![]() ,因为
,因为![]() 时,
时, ![]() ,所以
,所以![]() , 即恒有
, 即恒有 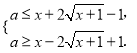 令
令![]() , 当
, 当![]() 时,
时, ![]() ,
, ![]() ,所以
,所以![]() , 所以
, 所以![]() , 所以
, 所以![]() .
.
② 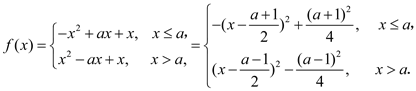
![]() 当
当![]() 时,
时, ![]() ,
,
这时![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() ;
;
![]() 当
当![]() 时,
时, ![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
, 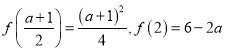 ,
,
而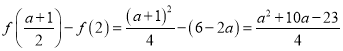
![]() ,
,
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, 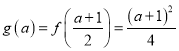 ;
;
![]() 当
当![]() 时,
时, ![]() ,
,
这时![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,此时
上单调递减,此时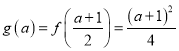 ;
;
![]() 当
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() ;
;
综上所述, ![]() 时,
时, 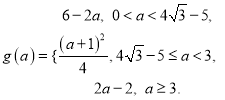
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,函数
,函数 .
.(1)求
 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;(2)若
 ,
,  ,求
,求 的值;
的值;(3)若函数
 在区间
在区间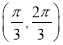 上是单调递增函数,求正数
上是单调递增函数,求正数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.

(Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.

(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知圆M:(x+1)2+y2=
 的圆心为M,圆N:(x﹣1)2+y2=
的圆心为M,圆N:(x﹣1)2+y2=  的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点(1,0)的直线l与曲线P交于A,B两点,若 =﹣2,求直线l的方程.
=﹣2,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣1)2﹣
 .
.
(Ⅰ)求函数的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2 , 证明x1+x2>2.
相关试题

