【题目】在平面直角坐标系xOy中,已知圆M:(x+1)2+y2= ![]() 的圆心为M,圆N:(x﹣1)2+y2=
的圆心为M,圆N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点(1,0)的直线l与曲线P交于A,B两点,若 ![]() =﹣2,求直线l的方程.
=﹣2,求直线l的方程.
参考答案:
【答案】解:(Ⅰ)设动圆P的半径为r,则|PM|= ![]() ﹣r,|PN|=r+
﹣r,|PN|=r+ ![]() .
.
两式相加,得|PM|+PN|=4>|MN|,
由椭圆定义知,点P的轨迹是以M、N为焦点,焦距为2,实轴长为4的椭圆,其方程为 ![]() .
.
(Ⅱ)当直线的斜率不存在时,直线l的方程为x=1,则 ![]() ,
, ![]() ,
, ![]() .当直线的斜率存在时,设直线l的方程为y=k(x﹣1),设A(x1,y1),B(x2,y2),联立
.当直线的斜率存在时,设直线l的方程为y=k(x﹣1),设A(x1,y1),B(x2,y2),联立 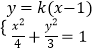 消去y,得(3+4k2)x2﹣8k2x+4k2﹣12=0,则有
消去y,得(3+4k2)x2﹣8k2x+4k2﹣12=0,则有 ![]() ,
, ![]() ,
, ![]() =
= ![]() =
= ![]() .
.
由已知,得 ![]() ,解得
,解得 ![]() .
.
故直线l的方程为 ![]()
【解析】(Ⅰ)根据两圆内外切的性质可得出|PM|+PN|=4>|MN|,即为椭圆由已知可求出方程。(Ⅱ)分情况讨论直线斜率存在和不存在,当斜率不存在时不成立;而当斜率存在时,设出直线方程和椭圆联立,消去y 由韦达定理求出 x 1 + x 2、 x1x2 的值,代入到向量的数量积坐标运算公式即可求出 k的值进而得出直线方程。
【考点精析】认真审题,首先需要了解椭圆的概念(平面内与两个定点![]() ,
,![]() 的距离之和等于常数(大于
的距离之和等于常数(大于![]() )的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距).
)的点的轨迹称为椭圆,这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.

(Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,函数
时,函数 恰有两个不同的零点,求实数
恰有两个不同的零点,求实数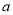 的值;
的值;(2)当
 时,
时,① 若对于任意
 ,恒有
,恒有 ,求
,求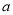 的取值范围;
的取值范围;② 若
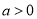 ,求函数
,求函数 在区间
在区间 上的最大值
上的最大值 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某化工厂拟建一个下部为圆柱,上部为半球的容器(如图,圆柱高为h,半径为r,不计厚度,单位:米),按计划容积为72π立方米,且h≥2r,假设其建造费用仅与表面积有关(圆柱底部不计),已知圆柱部分每平方米的费用为2千元,半球部分每平方米4千元,设该容器的建造费用为y千元.

(Ⅰ)求y关于r的函数关系,并求其定义域;
(Ⅱ)求建造费用最小时的r. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x﹣1)2﹣
 .
.
(Ⅰ)求函数的单调区间;
(Ⅱ)若函数f(x)有两个零点x1 , x2 , 证明x1+x2>2. -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司计划在甲、乙两座城市共投资240万元,根据行业规定,每个城市至少要投资80万元,由前期市场调研可知:甲城市收益
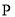 与投入
与投入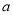 (单位:万元)满足
(单位:万元)满足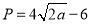 ,乙城市收益
,乙城市收益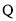 与投入
与投入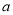 (单位:万元)满足
(单位:万元)满足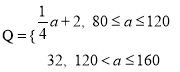 ,设甲城市的投入为
,设甲城市的投入为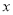 (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为 (单位:万元).
(单位:万元).(1)当投资甲城市128万元时,求此时公司总收益;
⑵试问如何安排甲、乙两个城市的投资,才能使公司总收益最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,b>0,且ab=1,则函数f(x)=ax与函数g(x)=﹣logbx的图象可能是( )
A.
B.
C.
D.
相关试题

